Chapitre 2 Approche formelle de lois de vitesse d'ordre simple

Réactions d'ordre global deux

2.3 Réaction d'ordre global 2 :
Réactions qui obéissent à une loi de vitesse ou 
suivant que l'ordre est 2 par rapport à un réactif ou que l'on a un ordre partiel 1 pour deux réactifs. 
  

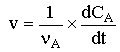
Pour une réaction du type 2.A = P   n A = - 2
La loi de vitesse étant d'ordre 2 par rapport à A on peut écrire :

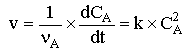
qui s'intègre en

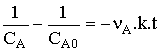
avec n_A = - 2  d'où 

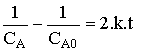( k en L mol-1 s-1 )

De l'expression précédente, on tire facilement la relation qui permet de calculer la concentration de A à un instant t : 

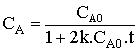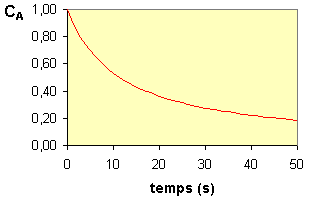
 La variation de C_A au cours du temps est représentée sur la figure ci-dessous :

Cliquez ici pour une comparaison des variations C_A pour des réactions d'ordre 1 et d'ordre 2.
Cliquez ici pour lire une remarque concernant l'écriture de l'équation bilan.
Cliquez ici pour examiner d'autres formes de la loi de vitesse.

Temps de demi-vie.
Le temps de demi-vie se déduit de la loi de vitesse intégrée en posant  d'où : 

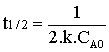Pour une réaction d'ordre 2, le temps de demi-vie est donc inversement proportionnel à la concentration. Voir figure ci-contre :

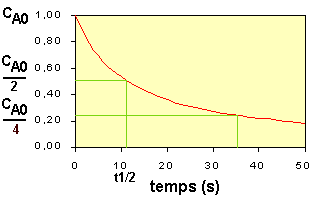
Le temps de demi-vie d'une réaction du second ordre est inversement proportionnel à la concentration du réactif. 

Cette observation n'est pas sans conséquences en ce qui concerne la dégradation de substances toxiques dans l'environnement.  Les substances qui se décomposent suivant une réaction du second ordre mettront beaucoup plus de temps pour s'éliminer que celles qui subissent des dégradations du premier ordre.

 

Vérification de l'ordre 2.

Position du problème :
On étudie une réaction et on désire s'assurer qu'elle suit une loi du second ordre. Si c'est bien le cas, on désire généralement déterminer la valeur du coefficient de vitesse. Dans ce qui suit, on examineraseulement le cas d'un ordre deux par rapport à un seul réactif. Le cas des réactions d'ordre global deux faisant intervenir deux réactifs avec un ordre partiel égal à un pour chacun d'eux est traité dans le paragraphe suivant.

On peut effectuer cette vérification à partir :

	des valeurs des temps de demi-vie,
	des valeurs des vitesses correspondantes à différentes concentrations,
	des valeurs de concentrations mesurées au cours du temps.

     
Vérification de l'ordre 2
à partir des valeurs des temps de demi-vie :
Le temps de demi-vie d'une réaction du second ordre est inversement proportionnel à la concentration du réactif.

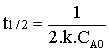
On peut vérifier qu'une réaction est d'ordre deux en s'assurant que, pour plusieurs concentrations C_A0 , le produit  est constant.

Remarque :
Cette vérification peut porter sur plusieurs expériences effectuées avec des concentrations initiales différentes, ou sur une expérience au cours de laquelle on a déterminé plusieurs valeurs du temps de demi-vie.

Vous pouvez voir des exemples...

     
Vérification de l'ordre 2
à partir des valeurs des vitesses correspondantes à différentes concentrations :
Par définition, la vitesse d'une réaction du second ordre s'écrit :

On peut donc vérifier qu'une réaction est d'ordre deux en s'assurant que sa vitesse est proportionnelle au carré de la concentration.

Remarque :
Cette vérification peut porter sur plusieurs expériences effectuées avec des concentrations initiales différentes (dans ce cas on utilise souvent les vitesses initiales), ou sur une seule expérience au cours de laquelle on a déterminé la vitesse et la concentration à différents instants.

Vous pouvez voir des exemples...

     
Vérification de l'ordre 2
à partir des valeurs de concentrations mesurées au cours du temps :
La forme intégrée de la loi de vitesse du second ordre s'écrit :

Remarque :
Cette vérification peut se faire de manière numérique, en calculant pour chaque couple C_A,t la valeur du coefficient de vitesse et en s'assurant qu'elle est constante,  ou de manière graphique, en traçant 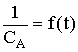 qui doit donner une droite.

Vous pouvez voir des exemples...

Réactions d'ordre global deux

Ordre partiel 1 par rapport à deux réactifs

2.3.2 Ordre partiel 1 par rapport à deux réactifs.

Dans une première approche on se limite ici au cas des réactions du type : A + B = Produits   avec 

donc d'ordre global 2 et d'ordre 1 par rapport à chaque réactif.

Loi de vitesse :

On distingue deux cas : celui pour lequel les concentrations initiales sont différentes et le cas particulier simple qui se présente lorsque les concentrations initiales sont égales C_A0 = C_B0

Dans le cas particuler pour lequel les concentrations sont égales, les concentrations au cours du temps restent alors égales CA = CB et la loi de vitesse est la même que précédemment :  d'où la même expression intégrée.

A savoir :  k en L mol-1 s-1

Lorsque les concentrations initiales sont différentes :  C_A0 différent de C_B0

En posant x la concentration transformée à un instant t,
les concentrations courantes s'écrivent en fonction des concentrations initiales :   et  

La vitesse de réaction :   est égale à 
d'où l'expression de la loi de vitesse sous sa forme différentielle qui s'intègre en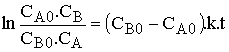  

Cliquez ici pour voir des détails sur l'intégration.