Analyse 1 Etude locale des fonctions de la variable réelle Fonction continue en un point Continuité et opérations

Thèorème. Opérations algébriques. Si f et g sont continues en x0, alors f+g, fg et, si g(x0)0, f/g sont continues en x0.

Preuve: On montre que 1/g est continue en x₀ tel que g(x₀)0, les autres démonstrations sont analogues.
On montre d'abord que si g(x₀)0, alors g(x) est minorée en valeur absolue par un nombre strictement positif dans un voisinage de x₀.
On utilise ensuite cette minoration pour majorer 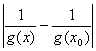(Preuve).

Conséquences

• Les fonctions polynômes : x P(x) (PR[X]) sont continues en tout point de R.
• Les fonctions rationnelles: x P(x)/Q(x) avec P, Q R[X], (Q différent du polynôme nul) sont continues en tout point de leur ensemble de définition.
• Dans l'espace vectoriel F(I,R) des applications d'un intervalle I dans R, le sous ensemble des fonctions continues en un point x₀ de I en est un sous espace vectoriel.

Thèorème. Composition des applications. Soit f et g des fonctions définies respectivement sur des intervalles ouverts I et J; on considère un point x0I tel que f(x0)J. Alors, si f est continue en x0 et g continue en u0=f(x0), gof est continue en x0.

Preuve : Cela repose sur l'écriture symbolique de la continuité (Preuve).

(Exemples)

Groupe MMM Maths UPI Université Pierre et Marie Curie (Paris 6)

Analyse 1 Etude locale des fonctions de la variable réelle Fonction continue en un point Continuité et opérations