Analyse 1 Suites de nombres réels Définitions, propriétés élémentaires Suite extraite

Extraire une suite d'une suite donnée c'est prendre, dans l'ordre, certains termes de la suite.

Définition. Soit une suite réelle ; on appelle suite extraite de une suite obtenue en composant avec une application strictement croissante de N dans N. On obtient ainsi la suite où .

Exemples
Soit une suite réelle ;
- soit : N N, n 2n la suite extraite obtenue est la suite des termes d'indice pair ;
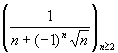- soit : N N, n 2n+1 la suite extraite obtenue est la suite des termes d'indice impair. Ainsi si l'on considère la suite , la suite des termes d'indice pair est la suite , la suite des termes d'indice impair est .
De même la suite () est extraite de la suite (2ⁿ), l'application étant l'application nn!.

Groupe MMM Maths UPI Université Pierre et Marie Curie (Paris 6)