|
|
 |
|
|
|
| Définition. Soit  une suite réelle ; on dit
que est convergente (ou converge)
s'il existe un réel  tel que converge vers .Sinon est divergente (ou diverge). |
Une suite convergente est donc caractérisée par la proposition :
;
ainsi les suites 
et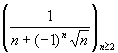 
sont convergentes, le réel satisfait, pour chacune, à la condition.
Exprimer qu'une suite est divergente revient à exprimer que, pour tout réel, la suite ne converge pas vers ce réel ou encore écrire la négation de la proposition précédente :
;
ainsi la suite 
est divergente en
effet :
soit un réel,
si
alors pour
,
sialors pour
= 1 et n = N ou N + 1 on a
.
La nature d'une suite (convergence ou divergence) ne dépend que de son
comportement quand 
; on dit
encore à partir d'un certain rang. On peut en particulier modifier les termes
d'une suite pour un nombre fini d'indices sans en changer la nature.
| Proposition. Toute suite convergente est bornée. |
Preuve : Une valeur déterminée de donne un encadrement de |un| pour n>N.
On en déduit une majoration de |un| pour tout n
(Preuve).
Groupe MMM Maths UPI Université Pierre et Marie Curie (Paris 6)
|
|
|
