|
|
 |
|
|
|
Dans tout le paragraphe on notera I un intervalle de R non vide ni réduit à un point.
| Définition. Soit f une application de I dans R, on dit que f est dérivable sur I si f est dérivable en tout point de I. On note alors :
f’ est l’application dérivée de f ou plus simplement la dérivée de f. |
.
| Définition. Si la fonction f’ est continue sur I on dit que f est continûment dérivable sur I ou de classe C1sur I. On note C1(I,R) l’ensemble des fonctions de classe C1sur I. |
Compte-tenu de ce qui a été vu à propos des fonctions
dérivables en un point, on déduit immédiatement de la
définition précédente que les polynômes, les fonctions
sinus, cosinus et l'exponentielle sont de classe C1
sur R, ainsi que les fonctions rationnelles sur tout intervalle qui
ne contient pas de pôle (zéro du dénominateur),les fonctions
logarithme et racine carrée sur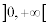 
, la fonction tangente sur 
.
Groupe MMM Maths UPI Université Pierre et Marie Curie (Paris 6)
|
|
|
