|
|
 |
|
|
|
| Définition. Si n est
un entier positif ou nul, on définit, si elle existe, la dérivée nième de f, en posant
par convention :
|
On note encore 
.
Définition. Si la
dérivée d’ordre n de f existe, on dit que f est n fois dérivable sur I, si f (n)
est continue sur I on dit que f est de classe Cn sur I. Si f est, pour tout
entier n, n fois dérivable, on dit que f est indéfiniment dérivable sur I ou de classe  sur I. |
sur
R, ainsi que les fonctions rationnelles sur tout intervalle qui ne
contient pas de pôle (zéro du dénominateur),les fonctions
logarithme et racine carrée sur 
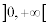, la fonction tangente sur 
.| Théorème : Formule
de Leibniz.
Si f et g sont des fonctions n fois dérivables sur I,alors la fonction fg est n fois dérivable sur I et :
|
Groupe MMM Maths UPI Université Pierre et Marie Curie (Paris 6)
|
|
|
