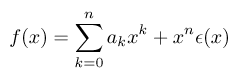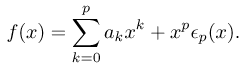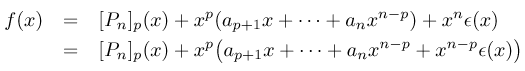Développements limités Définitions et propriétés Restriction d'un développement limité

Soit P_n (x) = a₀ + a₁ x + ... + a_n x ⁿ ; pour tout 0 £ p £ n on note [P_n]_p le polynôme [P_n]_p (x) = a₀ + a₁ x + ... + a_p x ^p , c'est à dire le polynôme obtenu en supprimant dans P_n (x) tous les termes de degré supérieur à p ; on dit parfois que l'on a tronqué P_n à l'ordre p. Ce polynôme [P_n]_p est appelé "restriction de P_n à l'ordre p" ou bien "polynôme P_n tronqué à l'ordre p."

Cette notion permet de diminuer l'ordre d'un développement limité donné.

Proposition 1

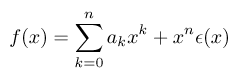
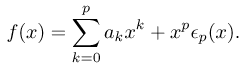
Si f admet un développement limité à l'ordre n, alors f admet un développement limité à tout ordre p £ n, On dit que ce développement est obtenu en tronquant à l'ordre p le développement donné.

Preuve
En effet, soit f(x) = P_n (x) + x ⁿ e (x) (avec lim_{x ® 0} e (x) = 0) un développement limité de f à l'ordre n en 0. On peut écrire :

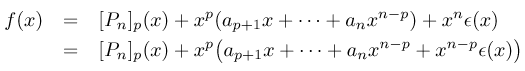
Posons e_p (x) = a_p+1 x + ... + a_n x ^n-p + x ^n-p e_p (x) ; comme lim_x ® 0 e_p = 0, on a obtenu un développement limité à l'ordre p en 0.

Développements limités Définitions et propriétés Restriction d'un développement limité