|
Jusqu'ici, on aurait pu imaginer qu'une fonction donnée ait plusieurs développements limités à l'ordre 4 par exemple, ou bien plusieurs développements limités à l'ordre 7, etc. Cela ne peut pas arriver comme l'exprime le théorème suivant :
Théorème 1
| Si f admet un développement limité à l'ordre n en 0, alors ce développement limité est unique. |
Preuve
Soit f(x) = P(x) + x n e1 (x) et f(x) = Q(x) + x n e2 (x) deux développements
limités de f à l'ordre n en 0 ; montrons que P = Q (on aura alors e1 = e2). On raisonne par récurrence sur l'ordre n :
limx ® 0 f(x) = a0 = b0.
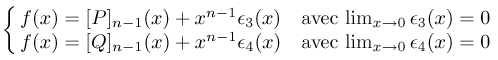
sont deux développements limités de f à l'ordre (n - 1) en 0 donc, d'après l'hypothèse de récurrence,
Puisque P(x) = [P]n-1 (x) + an x n et Q(x) = [Q]n-1 (x) + bnx n , il reste à montrer que an = bn ; il suffit de remarquer que :
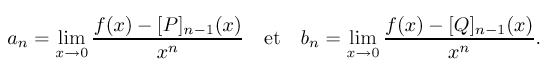
Dans la suite, lorsque f possèdera un développement limité à l'ordre n en 0, nous parlerons du développement limité de f à l'ordre n en 0.