|
Lorsque f est de classe C n+1 sur un voisinage de 0, f possède un développement limité à l'ordre n en 0. Mais la réciproque est fausse en général comme on va le voir ; on a quand même le résultat suivant :
Proposition 3
| Soit f définie sur un voisinage pointé de 0 ; on suppose que f possède un développement limité à l'ordre n en 0, avec n ³ 1. Alors on peut prolonger f en 0, en une fonction dérivable au point 0. |
Preuve
En effet, pour tout x Î V*(0) : f(x) = a0 + a1 x + ... + an x n + x n e (x).
Posons f(0) = a0, alors :
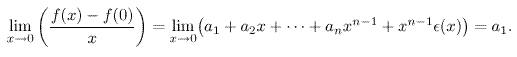
La fonction f, ainsi prolongée, est donc dérivable en 0, et de plus f ' (0) = a1 :
Exemple : 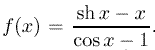 On peut montrer que f admet développement limité à l'ordre n en 0, pour tout n Î
On peut montrer que f admet développement limité à l'ordre n en 0, pour tout n Î ![]() ; en particulier pour n = 2 :
; en particulier pour n = 2 :
f(x) = - 1/3 x + x 2 e (x). En posant f(0) = 0, on prolonge f en une fonction dérivable au point 0 (f '(0) = - 1/3).
Cependant, de manière générale, l'existence, pour f, d'un développement limité à un ordre n ³ 2 en 0, n'entraîne pas des propriétés de dérivabilité à des ordres k ³ 2. Regardons, par exemple, la fonction f définie par :
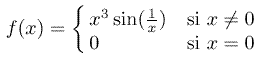
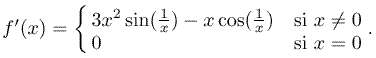
Mais f n'est pas deux fois dérivable au point 0, car : ![]() n'a pas de limite lorsque x tend vers 0.
n'a pas de limite lorsque x tend vers 0.