|
 |
 |
|
|
|
Somme de 2 s.e.v. : Définition et théorème
Comme la réunion de deux sous-espaces vectoriels n'est pas en général un sous-espace vectoriel, il est utile de connaître les sous-espaces vectoriels qui contiennent ces deux sous-espaces vectoriels, et en particulier le plus petit d'entre eux (au sens de l'inclusion).
|
Définition de la somme de deux sous-espaces Si F et G sont deux sous espaces vectoriels d'un K-espace vectoriel E, l'ensemble de tous les éléments
|
Remarque :
L'ensemble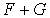 
contient
F et contient
G : en effet tout élément
x de
F s'écrit 
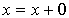avec x appartenant à F
et 0 appartenant à G (puisque G
est un sous-espace vectoriel), donc x appartient
à 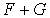. De même pour un élément de G.
|
Théorème de structure de la somme de deux sous-espaces vectoriels
|
Cliquez moi pour voir la preuve !
Preuve
du 2
D'après la remarque précédente et la partie 1 du théorème, 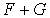est un sous espace vectoriel contenant 
.
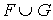Il reste à démontrer que tout sous-espace vectoriel contenant 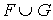contient aussi .
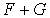Considérons H, un sous-espace vectoriel de E contenant 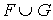, et u un élément quelconque de .
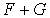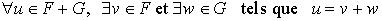
L'élément u est donc la somme d'un élément v de F et d'un élément w de G.
Les éléments v et w appartiennent à 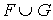, donc ils appartiennent aussi à H, et comme H est un sous-espace vectoriel, l'élément 
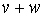appartient à H donc 
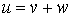est un élément de H. Donc H contient .
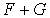Cas
particulier : Somme de deux sous-espaces engendrés par des parties
finies
|
Propriété de génération de la somme Si  |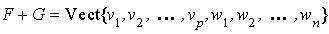
La preuve est laissée au lecteur à titre d'exercice
(ou consulter la ressource : "Sous-espaces vectoriels de type fini").
|
|
|
où x est un élément de F et y un élément de G, est appelé somme des sous-espaces vectoriels F et G . Cette somme est notée 
et 
, alors