|
 |
 |
|
|
|
Somme de 2 s.e.v. : Exemples dans R3
Exemple
1
Déterminons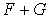 
dans le cas où F et G sont les sous-espaces vectoriels de R3 suivants :
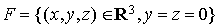
et
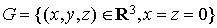
Un élément u de 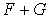s'écrit 
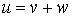où v est un élément de F et w un élément de G ; donc il existe deux nombres réels x et y tels que 
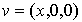et 
:
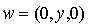donc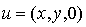 
.
Réciproquement un tel élément 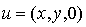est la somme de 
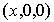et de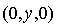 
.
Donc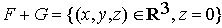 
.
Exemple
2
Soient F' et G' les deux sous-espaces vectoriels de R3 suivants :
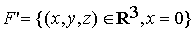
et
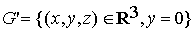
Dans cet exemple, montrons que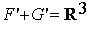 
.
Par définition de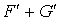 
, tout élément
de 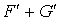est contenu dans R3;
mais réciproquement si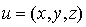 
est un élément
quelconque de R3 :
, .
|
|
|
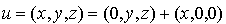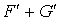