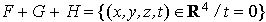|
 |
 |
Somme de plusieurs sous-espaces vectoriels
La notion de somme de deux sous-espaces vectoriels d'un K-espace vectoriel se généralise en la notion de somme de plusieurs sous-espaces.
|
Définition de la somme de n sous-espaces vectoriels Si 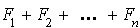 ou ou 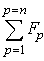 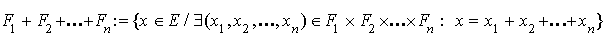 |
|
Théorème de structure de la somme de n sous-espaces vectoriels La somme |
La démonstration est analogue au cas n = 2.
 Exemple
immédiat
Exemple
immédiat
Considérons dans R4 les
trois sous-espaces vectoriels F, G et H, engendrés respectivement
par
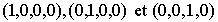 , alors tout élément de la
somme
, alors tout élément de la
somme 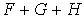 s'écrit sous la
forme
s'écrit sous la
forme 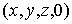 et donc :
et donc :