|
 |
 |
Somme directe de deux sous-espaces vectoriels
Dans l'exemple 2 précédent : 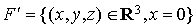 et
et 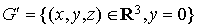
(ce qui entraîne 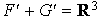 ) un élément quelconque
) un élément quelconque 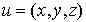 de
de 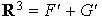 peut s'écrire comme somme d'un élément de F' et d'un élément de G' de plusieurs manières, par exemple :
peut s'écrire comme somme d'un élément de F' et d'un élément de G' de plusieurs manières, par exemple :
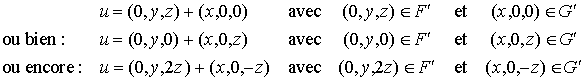
L'écriture de u comme somme d'un élément de F' et d'un élément de G' n'est pas unique.
Par contre, dans l'exemple 1 :
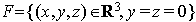 et
et 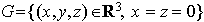 ,
un élément quelconque
,
un élément quelconque 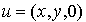 de
de 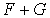 ne
peut s'écrire que d'une manière unique comme somme d'un élément de F et
d'un élément de G, à savoir :
ne
peut s'écrire que d'une manière unique comme somme d'un élément de F et
d'un élément de G, à savoir :
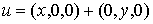
|
Définition de la somme directe de deux sous-espaces Etant donnés deux sous-espaces vectoriels F et G de E, la somme La somme |
Remarque :
On dit que l'élément u de 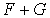 s'écrit d'une manière unique
comme somme d'un élément de F et d'un élément de G lorsque la propriété suivante est
vérifiée :
s'écrit d'une manière unique
comme somme d'un élément de F et d'un élément de G lorsque la propriété suivante est
vérifiée :
l'élément u de 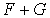 n'est égal à la fois à
n'est égal à la fois à 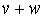 et
à
et
à 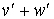 ( où v et v' sont des éléments de F,
w et w' des éléments de G) que dans le cas où
( où v et v' sont des éléments de F,
w et w' des éléments de G) que dans le cas où 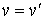 et
et 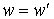 :
:
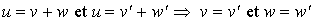
|
Propriété caractéristique Une condition nécessaire et suffisante pour que la somme de deux sous-espaces vectoriels F et G soit directe est que l'intersection de F et de G soit réduite au vecteur nul. 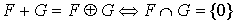 |
 Preuve
Preuve
 Supposons
que
Supposons
que 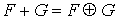 .
.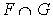 alors u peut s'écrire des
deux manières suivantes, comme somme d'un élément de F et d'un élément de G :
alors u peut s'écrire des
deux manières suivantes, comme somme d'un élément de F et d'un élément de G :

L'élément u étant un élément de 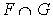 , est donc un élément de
, est donc un élément de 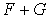 ; d'après l'unicité de
l'écriture d'un élément de
; d'après l'unicité de
l'écriture d'un élément de 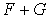 , cela entraîne :
, cela entraîne : 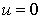 .
Donc
.
Donc 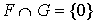 .
.
 Réciproquement
supposons que
Réciproquement
supposons que 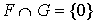 .
.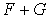 . Si u s'écrit de
deux manières comme la somme d'un élément de F et d'un élément de G :
. Si u s'écrit de
deux manières comme la somme d'un élément de F et d'un élément de G :
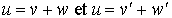 , où v et v' sont des éléments de F et
w et w' des éléments de G, alors
, où v et v' sont des éléments de F et
w et w' des éléments de G, alors 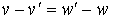 ; mais
; mais 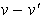 est
un élément de F et
est
un élément de F et 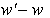 est un élément de G (puisque F et G sont des sous-espaces
vectoriels) donc
est un élément de G (puisque F et G sont des sous-espaces
vectoriels) donc 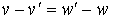 est un élément de
est un élément de 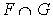 , c'est donc l'élément nul,
donc
, c'est donc l'élément nul,
donc 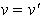 et
et 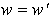 .
.
L'écriture de u comme somme d'un élément de F et d'un élément de G est donc unique.