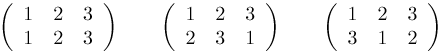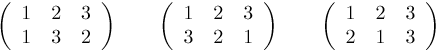On désigne pour des raisons que nous expliquerons dans un paragraphe suivant, et
on note les permutations des nombres 1, 2, 3 de la façon suivante :
Permutations paires
Permutations impaires
On posera :
eijk = + 1 si i, j, k est une permutation paire de {1, 2, 3}.
eijk = - 1 si i, j, k est une permutation impaire de {1, 2, 3}.
On peut donc résumer les relations obtenues précédemment avec líégalité :
det(ei, ej, ek) = eijk det(e1, e2, e3)