Si les vecteurs A, B, C sont dépendants, alors le déterminant det(A, B, C) est
nul. En effet, si l’un des vecteurs par exemple A, s’exprime en fonction des autres
A = lB + mC et donc det(lB + mC, B, C) = 0
Réciproque
Si det(A, B, C) = 0, alors les vecteurs A, B, C sont dépendants. On démontre la
contraposée : si A, B, C sont indépendants, alors det(A, B, C)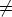 
0.
Si A, B, C sont indépendants, ces vecteurs forment une base de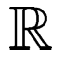 
3 et nous pouvons
exprimer e1, e2, e3 en fonction de A, B, C.
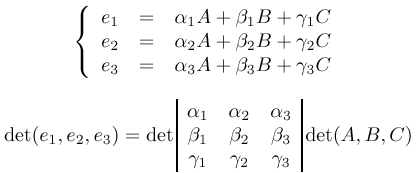
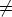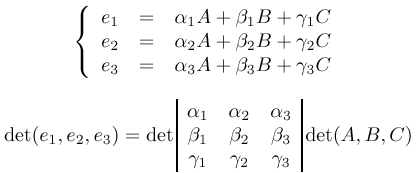
Or det(e1, e2, e3) = 1 et donc on peut déduire det(A, B, C) 0.
