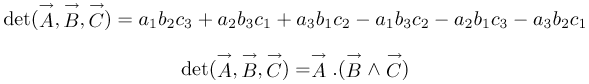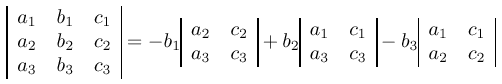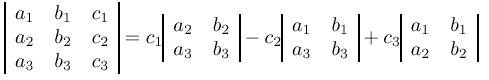Interprétation géométrique
Si on rapporte l’espace à un repère orthonormé direct. Le déterminant det(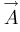 ,
, 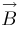 ,
, 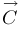 )
est le produit mixte de ces trois vecteurs
)
est le produit mixte de ces trois vecteurs 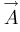 ,
, 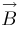 ,
, 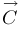 . Il s’interprète comme volume du
parallélépipède construit sur ces trois vecteurs.
. Il s’interprète comme volume du
parallélépipède construit sur ces trois vecteurs.
Cela se démontre en mettant les coordonnées de 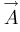 en facteur :
en facteur :
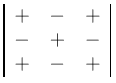
Modes de calcul du déterminant
Nous avons calculé le déterminant en développant par rapport à la première colonne.
De la même façon nous pouvons faire un développement par rapport à la deuxième
colonne ou à la troisième colonne dans l’expression :
a1b2c3 + a2b2c2 + a3b1c2 - a1b3c2 - a2b1c3 - a3b2c1
![]() en facteur :
en facteur :