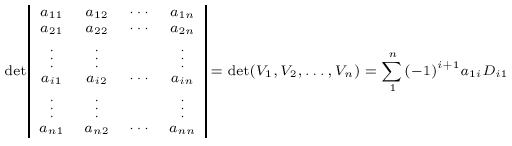Géométrie analytique Déterminant d'ordre n

Méthode de définition de proche en proche

Comme pour le déterminant d’ordre 3 calculé à partir des déterminants d’ordre 2, on va définir par récurrence le déterminant d’ordre n ou encore de n vecteurs de 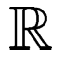. On définit le développement par rapport à la première colonne qui semble jouer un rôle privilégié. On verra qu’il n’en est rien.

Déterminant d’ordre n :

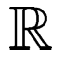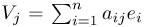soit E = ⁿ rapporté à la base canonique e₁, ..., e_n. On considère n vecteurs V₁, ...; V_n avec pour toute valeur de j, et on définit le déterminant de ces n vecteurs par récurrence sur n par l’expression :

Les déterminants D_i1 étant des déterminants d’ordre n - 1 obtenus en barrant dans le déterminant D la i-ième ligne et la première colonne.