| Intégration | Intégrale de Riemann | Propriétés | Théorème de la moyenne |
 |
 |
| Intégration | Intégrale de Riemann | Propriétés | Théorème de la moyenne |
|
|
Théorème de la moyenne, sommes de Riemann
|
Théorème. Si
f est intégrable sur alors
Si
f est continue sur
(formule dite première formule de la moyenne). |
Ce théorème montre que l’intégrale vérifie la condition 2 exposée dans le préliminaire.
Pourquoi formule de la moyenne ?
Pour tout entier n>0, soit sn la subdivision régulière d’ordre n ;
on considère un ensemble de points 
.
Alors l’expression 
représente la valeur moyenne de la fonction f aux points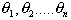 
.
On a alors le corollaire :
|
Corollaire 1: Si la fonction f est intégrable sur
Si
f est continue sur
|
Ceci justifie pour f(c) la dénomination
de valeur moyenne de la fonction f sur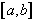 
.
Remarque :
les expressions de la forme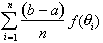 
sont des sommes
de Riemann de f relativement
à la subdivision sn.
Plus généralement, pour une fonction
f définie sur un intervalle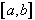 
,
on peut définir la somme de Riemann de f relative à
-
une subdivision
s quelconque de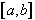 
:
et
-
un choix de points
.
Définition. On appelle somme de Riemann de f relative à s
et à l’ensemble de points 
le réel  . |
On a alors un second corollaire qui se démontre comme le premier.
Corollaire 2. Si
f est intégrable sur 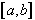 les
sommes de Riemann de f ont toutes pour limite
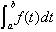 quand
le pas de la subdivision tend vers 0. |
Ceci signifie que :
pour tout e
> 0, il existe h > 0 tel que,
pour toute subdivision 
de
pas h<h
et pour toute famille 
on
ait :
.
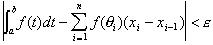Les applications de la "formule de la moyenne" sont nombreuses en particulier pour calculer la limite de suites de la forme :
.
| Intégration | Intégrale de Riemann | Propriétés | Théorème de la moyenne |
|
|
Groupe MMM Maths L'UTES Université Pierre et Marie Curie (Paris 6)
et si l’on pose 
.
, alors
tel
que
.
, alors
.
, alors
tel
que
.
