Comment montrer que 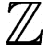 est dénombrable ?
est dénombrable ?
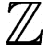 contient
contient  comme sous-ensemble,
donc sa puissance est au moins celle des entiers naturels.
comme sous-ensemble,
donc sa puissance est au moins celle des entiers naturels.
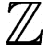 peut être construit en établissant une
relation d'équivalence sur les couples d'entiers positifs :
(a, b) est équivalent au couple (c, d) si a + d = b + c. Chaque
classe d'équivalence représente un entier relatif : la classe d'un
entier positif n admet un représentant du type (n, 0) et pour
l'entier négatif - n un représentant (0, n).
peut être construit en établissant une
relation d'équivalence sur les couples d'entiers positifs :
(a, b) est équivalent au couple (c, d) si a + d = b + c. Chaque
classe d'équivalence représente un entier relatif : la classe d'un
entier positif n admet un représentant du type (n, 0) et pour
l'entier négatif - n un représentant (0, n).
On peut ranger ces éléments en une suite de la façon
suivante :
(0, 0), (1, 0), (0, 1), (2, 0), (0, 2),
..., (n, 0), (0, n), ...
Cela montre que le cardinal de
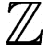 est égal à
est égal à 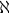 0, cardinal de
0, cardinal de  .
.
![]() est égal à
est égal à 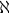 0, cardinal de
0, cardinal de ![]() .
.