La démonstration
de la dénombrabilité de  fut faite par Cantor en 1874.
fut faite par Cantor en 1874.
Comme l'ensemble  contient l'ensemble des
entiers, le cardinal de cet ensemble est au moins
contient l'ensemble des
entiers, le cardinal de cet ensemble est au moins 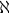 0.
0.
Il est facile de voir d'après la démonstration
précédente que si l'ensemble des nombres rationnels positifs
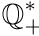 est dénombrable, l'ensemble
est dénombrable, l'ensemble  l'est
aussi.
l'est
aussi.
L'ensemble 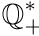 peut être construit en
établissant une relation d'équivalence sur l'ensemble des couples
d'entiers relatifs (a, b) avec a
peut être construit en
établissant une relation d'équivalence sur l'ensemble des couples
d'entiers relatifs (a, b) avec a 
 , b
, b

 et b
et b 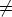 0 :
0 :
(a, b) ~ (c, d) si et
seulement si a d = b c.
Ceci est la façon mathématique d'exprimer que des
"fractions égales" représentent le même nombre rationnel qui admet
donc pour représentants une infinité de couples (numérateur,
dénominateur).
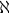 0.
0.


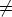 0 :
0 :