Logique Cardinal d'un ensemble Le continu : les réels

Le continu : les réels

L'ensemble des nombres réels peut être mis en bijection avec un intervalle, par exemple en utilisant la fonction tangente, et deux intervalles quelconques d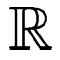e peuvent être mis en bijection en utilisant une fonction affine. Il suffit donc de montrer que l'ensemble des réels de l'intervalle ]0, 1[ est non dénombrable.

Chaque nombre réel compris entre 0 et 1 possède un développement décimal illimité ou deux. Les nombres non décimaux en ont un seul, les nombres décimaux possèdent deux développements : Par exemple :

0,95 = 0,95000... = 0,94999...

l'un comporte des 9 indéfiniment, on l'appelle développement impropre, l'autre, qu'on appelle développement propre, comporte seulement un nombre fini de chiffres non nuls après la virgule. Si on convient de n'utiliser que des développements propres, chaque nombre réel est donc associé à un unique développement propre ; si deux développements propres différent en un chiffre, ils sont les développements de nombres réels distincts.