|
|
|
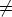 a00,
b1
a00,
b1 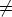 a11, b2
a11, b2 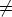 a22, etc. et que de plus les
bi ne soient pas égaux à des 9 indéfiniment.
a22, etc. et que de plus les
bi ne soient pas égaux à des 9 indéfiniment.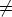 A0 car le premier chiffre après la virgule de
ces deux nombres diffère, B
A0 car le premier chiffre après la virgule de
ces deux nombres diffère, B 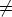 A1 car le deuxième chiffre
après la virgule de ces deux nombres diffère, B
A1 car le deuxième chiffre
après la virgule de ces deux nombres diffère, B 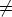 A2 car le
troisième chiffre après la virgule de ces deux nombres diffère,
etc. Le nombre B n'a pas été classé et on a obtenu une
contradiction.
On ne peut donc pas ranger les nombres
réels de l'intervalle ] 0,1 [ en une suite.
Cet ensemble n'est pas dénombrable. On en déduit immédiatement
que l'ensemble des nombres réels
A2 car le
troisième chiffre après la virgule de ces deux nombres diffère,
etc. Le nombre B n'a pas été classé et on a obtenu une
contradiction.
On ne peut donc pas ranger les nombres
réels de l'intervalle ] 0,1 [ en une suite.
Cet ensemble n'est pas dénombrable. On en déduit immédiatement
que l'ensemble des nombres réels