|
|
|
 |
 |
|
|
|
|
|
| Pour tout ensemble E, le cardinal de l'ensemble P(E) des parties de E est strictement supérieur au cardinal de E. |
On en fait une démonstration par l'absurde en supposant une application surjective f de E sur P(E), et on considère l'ensemble A :
A = {x 
E | x 
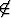f(x)}
Cet ensemble A est l'image d'un élément a de E par
l'application f. On constate alors que les deux assertions, a
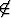A et a A sont impossibles. On a donc une
contradiction, ce qui démontre qu'il n'existe pas de surjection
d'un ensemble sur l'ensemble de ses parties.
