|
|
 |
 |
|
|
|
|
0 et c.
| L'affirmation "Il
n'existe pas de cardinal strictement compris entre 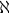0 et
c." est un axiome qui s'appelle l'hypothèse du
continu. |
On peut généraliser :
| L'affirmation "Pour tout cardinal infini e, il n'existe pas de cardinal strictement compris entre e et 2 e." est un axiome qui s'appelle l'hypothèse généralisée du continu. |
Gödel et Cohen ont aussi montré que cet axiome était indépendant des autres axiomes de la théorie des ensembles.
