DIPOLES ELECTRIQUES Action d'un champ électrique sur un dipôle

L'action en rotation engendrée par le champ sur le dipôle

Placée dans un champ électrique local E, chaque charge -q et +q du dipôle est soumise à une force de Coulomb. Compte tenu de la faible distance a entre les deux charges, nous considérerons que le champ électrique reste constant en direction et en intensité lorsque l'on se déplace de A en B.

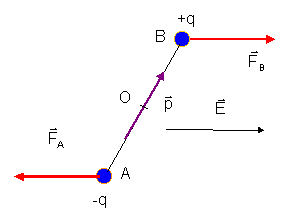
En A la charge -q est soumise à la force :

En B la charge +q est soumise à la force :

Notons que :

,

mais qu'il existe un couple ou action en rotation de ces forces non nul :

Appliquons ce calcul de l'action en rotation d'une force, à la détermination du couple créé par les forces :

En choisissant O le centre du dipôle comme centre de rotation il vient :

ou encore :

Le dipôle p placé dans le champ électrique subit une action en rotation ou couple de valeur :

Remarque : Nous avons, pour effectuer ce calcul, pris comme centre de rotation le point particulier O, milieu de AB. Choisissons un point quelconque O' du plan et calculons à nouveau le couple produit par les forces F_A et F_B par rapport à O'. Nous avons :

ou

soit

et il vient

Cet autre calcul du couple par rapport à un point quelconque montre que le moment créé par le champ électrique sur le dipôle est indépendant du point choisi comme centre de rotation. Nous avons donc :

• Le couple G tend à orienter le dipôle p parallèlement au champ électrique E. Lorsque le dipôle est parallèle et de même sens que le champ électrique le couple s'annule, il n'y a plus d'action en rotation.

Orientation d'un dipôle dans un champ

L'énergie potentielle électrique du dipôle dans un champ électrique

A l'échelle du dipôle, nous l'avons déjà mentionné, le champ électrique est à peu près constant.

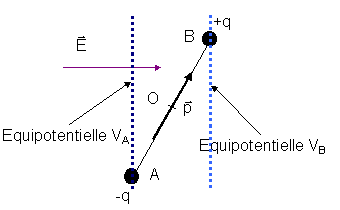
Perpendiculairement à la direction du champ électrique, il existe des équipotentielles V_A et V_B.

Calculons l'énergie potentielle du dipôle :

E_P = + q.V_B - q.V_A

= q(V_B - V_A)

Si nous revenons à la relation :

,

on peut aussi écrire :

 L'énergie potentielle du dipôle dans le champ électrique E s'exprime alors par :

soit :

• Le couple G tend à orienter le dipôle p parallèlement au champ électrique.

• Lorsque le dipôle p forme un angle a avec le champ électrique à E, l'énergie potentielle électrique prend une valeur :

E_{p min} = - p.E.cosa

• Lorsque le dipôle p est parallèle à E, l'énergie potentielle électrique prend une valeur minimum :

E_{p min} = - p.E.

Il est important de noter au cours de cette étude de l'interaction d'un champ électrique avec un dipôle, que le champ électrique E n'est pas en général le champ d'un laboratoire. Il s'agit dans la réalité souvent du champ électrique créé au niveau du dipôle par un autre dipôle. Deux molécules polaires sont ainsi en interaction par l'intermédiaire du champ électrique qu'une molécule polaire crée au centre de la molécule voisine et inversement

Les conclusions sur les interactions champ/dipôle nous permettent ainsi d'expliquer les orientations qu'un dipôle p₂ peut prendre dans l'environnement d'un dipôle p₁, comme représentées sur le schéma ci-dessous:

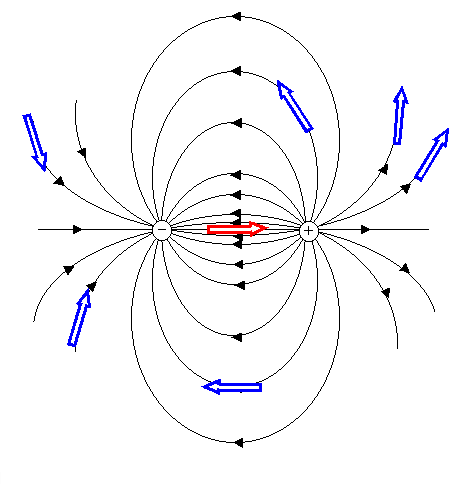
Le dipôle p₂ est en tout point parallèle au champ électrique créé par le dipôle p₁.

Dans le but de rendre minimum la valeur de l'énergie potentielle électrique il faut par ailleurs que le champ électrique soit le plus intense possible. Pour une même distance r correspondant à la distance intermoléculaire des deux molécules portant les dipôles p₁ et p₂, les positions A et B pour lesquelles le champ électrique est maximum sont des positions privilégiées. On note que les dipôles p₁ et p₂ sont alors parallèles.

Les lignes de champ du dipôle

Auteur : A.Cogne  1998

DIPOLES ELECTRIQUES Action d'un champ électrique sur un dipôle