|
|
 |
|
|
|
 |
Revenons sur la notion de
gradient et sur sa signification physique.
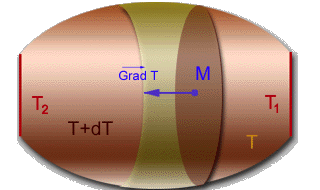
On peut associer un vecteur gradient à toute fonction continue de
points. Prenons l'exemple d'un matériau ayant une forme allongée
et imposons des températures constantes, T1 et T2
( )
, à ses extrémités.Après un certain temps, l'équilibre
thermique est réalisé : la température reste constante
en chaque point du matériau, mais elle varie évidemment d'un
point à un autre. La température est donc dans ce matériau
une fonction de la position du point d'observation. Une surface isotherme,
T, est le lieu des points où la température a la valeur T. |
Pour définir
le vecteur 
en un point M du matériau considérons la surface isotherme
T passant par ce point et la surface isotherme infiniment voisine, T + dT.
Le vecteur, ,
est porté par la normale en M à la surface isotherme, T. C'est
suivant cette direction que la variation de température est la plus
rapide, autrement dit que le gradient de température est le plus
élevé. Considérons en effet des déplacements
à partir d'un point quelconque P sur la surface isotherme T jusqu'en
des points de la surface isotherme T + dT. La variation correspondante de
température a pour ces déplacements la même valeur dT. |
|
 |
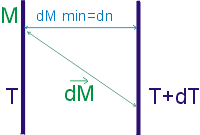Remarquons que la longueur des déplacements est
variable et est minimale suivant la direction de la normale. C'est donc suivant
cette direction que la variation de température est la plus rapide.
On la caractérise par le rapport |
|
|
|
de
l'augmentation de température, dT, à la distance minimale,
dn, qu'il faut parcourir pour l'observer. Par définition le module
du vecteur T est égal à ce rapport. Enfin, on convient de
l'orienter dans le sens des valeurs croissantes
de la température.