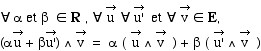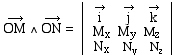Mécanique. Représentation de l'espace.7

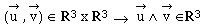
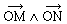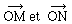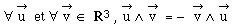
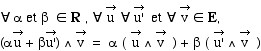
1.7. Produit vectoriel Définition intrinsèque Orientation de l'espace Définition extrinsèque Le produit vectoriel est une application de R3 x R3 dans R3 qui fait correspondre un vecteur à tout couple de vecteur de R3: Notation : désigne le produit vectoriel des vecteurs . Cette application possède les propriétés suivantes: • l' antisymétrie : • la bilinéarité : On définit le produit vectoriel de deux vecteurs - de façon intrinsèque, géométrique, sans référence à un repère, - de façon extrinsèque, par les composantes des vecteurs sur une base de l'espace R3. Définition intrinsèque Le produit vectoriel est le vecteur noté 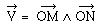. 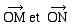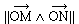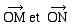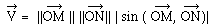• orthogonal au plan défini par les vecteurs , • de norme égale à l'aire arithmétique du parallélogramme construit sur soit • dont le sens est tel que le trièdre 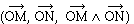soit direct. Le produit vectoriel de deux vecteurs est nul 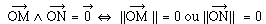ou bien 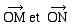sont colinéaires. L'orientation de l'espace est définie par le sens (arbitraire) d'un trièdre pris comme trièdre de référence. Si on change le sens du trièdre de référence, on change donc le sens du produit vectoriel qui en résulte. Pour définir le produit vectoriel , il est nécessaire de définir préalablement : - une mesure des longueurs - une mesure des angles - une orientation de l'espace.   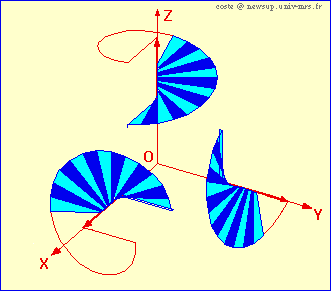L'animation ci-dessous montre l'orientation de l'espace à trois dimensions.   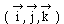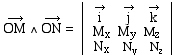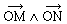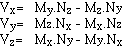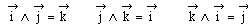L'orientation de l'espace   L'animation ci-dessous montre l'orientation du plan L'orientation du plan   Définition extrinsèque Elle nécessite d'exprimer les vecteurs et sur une base : Soit une base orthonormée et directe dans laquelle les vecteurs sont représentés par leurs composantes les composantes de sont : En particulier :   L'animation ci-dessous montre la variation du produit vectoriel de deux vecteurs lorsque leur angle varie. Produit vectoriel

Mécanique. Représentation de l'espace.7