Mécanique. Représentation de l'espace. 8

1.8. Coordonnées cartésiennes Dans la base cartésienne (encore appelée base canonique), les composantes du vecteur position 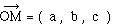sont identiques aux éléments du triplet qui constituent dans ce cas, les trois coordonnées du point M. Le vecteur position s'exprime alors 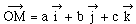. Remarque: Dans les autres bases, les trois composantes du vecteur position, obtenues par le produit scalaire de ce dernier par chaque vecteur de base, ne sont plus identiques aux coordonnées du point M. 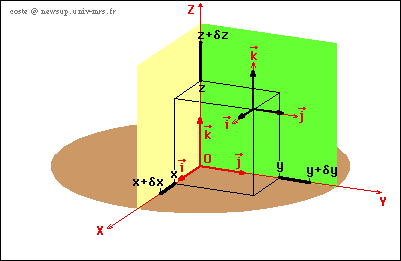L'animation ci-dessous montre l'ensemble du repérage cartésien : de la base, des coordonnées et de leurs accroissements élémentaires Vecteur élémentaire en coordonnées cartésiennes

Mécanique. Représentation de l'espace. 8