|
 2.3.Méthodes
d'intégration
Equations
à variables séparables
Equations différentielles linéaires
Règles
Il est toujours bon de chercher s'il est
possible d'abaisser l'ordre d'une équation en changeant de fonction.
Ainsi, l'équation du second ordre
en f : f " + f ' = 0 peut se ramener à une équation
du premier ordre en u en posant: f ' = u , d'où u '
+ u = 0
 2.3.1.Equations
à variables séparables
Ce sont des équations du premier
ordre de la forme
f ' F(f)
+ y
= 0
ce qui s'écrit plus couramment: f
'(x) .F(f(x))
+ y(x)
= 0 ou encore
y ' F(y)
+ y
(x) = 0
Leur résolution est immédiate
sachant que y ' = dy/dx :
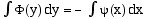d'où on tire y(x) après
intégration.
Remarque :
Tous les calculs de primitives correspondent
en fait à la résolution d'équations différentielles
à variables séparables.
2.3.2.Equations
différentielles linéaires
Ce sont des équations du type:
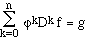
où Dk est un opérateur
de dérivation d'ordre k.
Soit J
l'ensemble des fonctions de R
-> R.
On définit l'application W
: J -> J
par
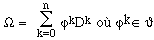
Alors,
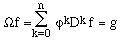
et l'équation linéaire s'écrit:
Wf
= g
Propriétés:
• W
est une application linéaire.
Si de plus, g = 0, l'équation
est dite linéaire et homogène.
Si g diffère de 0,
on appelle équation
homogène associée à
Wf
= g, la relation (quelquefois appelée équation
sans second membre) Wf
= 0
On montre que:
• l'ensemble
des solutions d'une équation différentielle linéaire
et homogène d'ordre n constitue un espace vectoriel.
• cet
espace vectoriel de fonctions est de dimension n, égale à
l'ordre de l'équation.
|
|
Règle
1:
Pour résoudre
une équation différentielle linéaire et
homogène d'ordre n, il suffit d'en trouver n solutions
particulières linéairement indépendantes.
La solution
générale est combinaison linéaire de ces
n solutions particulières
|
Si f1
et f2
sont deux solutions particulières de Wf
= g, et si a et b sont deux scalaires quelconques, a f1
+ b f2
est solution de Wf
= 0.
|
|
Règle
2
Pour résoudre
une équation différentielle linéaire, il
suffit de résoudre l'équation homogène
associée et de trouver UNE solution particulière
de l'équation complète.
La solution
générale de l'équation complète
est égale à la solution générale
de l'équation homogène associée plus la
solution particulière trouvée de l'équation
complète.
|
Autrement dit, étant
donnée fp
solution particulière de Wf
= g, f en est solution si et seulement s'il existe f0
solution de Wf
= 0 telle que f = fp
+ f0
|
