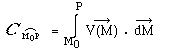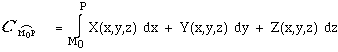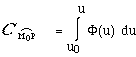Mécanique. Champs de vecteurs - Potentiel . 2

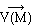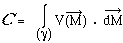
3.2. Circulation d'un champ de vecteurs Définition Circulation d'un champ de vecteurs dans un déplacement fini    3.2.1.Définition. La circulation du champ de vecteurs le long d'une courbe (g), est l'intégrale curviligne calculée le long de (g) ; sa valeur dépend en général du chemin suivi.    3.2.2.Circulation d'un champ de vecteurs dans un déplacement fini. On examine ici le cas où le champ de vecteurs dépend du point où on la considère. 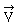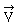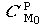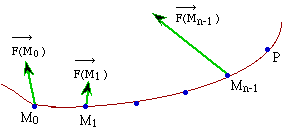Soitun champ de vecteurs; on étudie la circulation de pour un déplacement M0P de valeur finie, sur l'arc de courbe (g) que l'on note L'arc 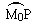peut s'approcher par un contour polygonal composé d'un grand nombre de parties rectilignes, cordes de petits arcs de (g), soit M0M1, M1M2,......, Mn-1P. 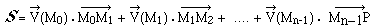La somme des circulations élémentaires de dans chacun des déplacements partiels, en considérant comme constant sur chacun d'eux s'écrit : S est une approximation de 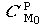. Pour améliorer cette approximation, on peut diviser l'arc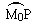en un nombre de plus en plus grand de parties, chacune d'elles tendant vers 0. Le contour polygonal tend vers (g), chaque élément de contour tend vers 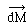. A la limite, la somme tend vers l'intégrale curviligne le long de (g) de 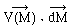. 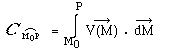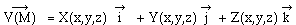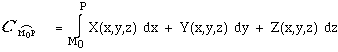La circulation du champ de vecteurs sur l'arc de courbe a pour définition En coordonnées cartésiennes, si le champ de vecteurs s'écrit en fonction des composantes X, Y, Z, fonctions scalaires des trois variables x, y, z: La circulation s'exprime alors : Cette intégrale curviligne est calculée de M0 en P suivant l'arc de courbe (g) et dans ce sens. Remarques : Si la courbe (g) est définie par les équations paramétriques: x = f(u), y = g(u), z = h(u), X,Y,Z,dx,dy,dz peuvent s'exprimer en fonction de la seule variable u. La circulation s'écrit alors : 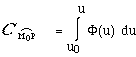   Le calcul de l'intégrale ci-dessus s'effectue en remplaçant x,y,z par leurs expressions et en intégrant entre les limites u0 et u qui correspondent à l'origine et à l'extrémité de l'arc d'intégration (g). Dans le cas le plus général, la valeur de l'intégrale dépend du contour le long duquel elle est calculée .

Mécanique. Champs de vecteurs - Potentiel . 2