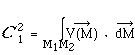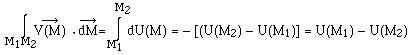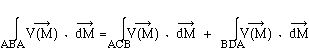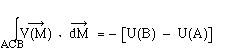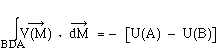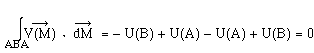Mécanique. Champs de vecteurs - Potentiel. 3

3.3. Fonction Potentiel Définition de la fonction potentiel Circulation le long d'un contour fermé Surfaces équipotentielles Exemples de champs    3.3.1. Définition de la fonction potentiel En général la circulation le long du segment curviligne M1M2 de la courbe (g) dépend non seulement des extrémités du chemin suivi, mais aussi de ce chemin lui-même : Si est un champ, en chaque point M de la courbe, il existe un vecteur champ ; au cours du déplacement élémentaire , la circulation élémentaire de ce champ est S'il existe une fonction U(M) telle que: alors : et la circulation du vecteur champ ne dépend que des valeurs prises par la fonction U(M) , si elle existe, aux extrémités du chemin suivi. La fonction U(M) est appelée fonction potentiel scalaire du vecteur champ Le champ dérive d’une fonction potentiel scalaire U(M), si la circulation de entre deux points quelconques M1 et M2 ne dépend pas du chemin suivi.    3.3.2. 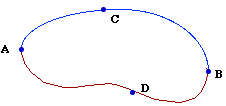Circulation le long d'un contour fermé La circulation le long du contour ABA est la somme de deux circulations : le long de ACB le long de BDA Si dérive d'un potentiel U(M):     Si le champ de vecteurs dérive d'un potentiel, sa circulation le long d'un contour fermé est nulle. On note etse lit : intégrale curviligne le long d'un contour fermé (g).     3.3.3. Surfaces équipotentielles    Le lieu des points pour lesquels la fonction potentiel a la même valeur U(M) = Cte est une surface équipotentielle. La fonction U(M) , si elle existe, ne peut prendre qu'une seule valeur au point M, il ne passe donc qu'une seule équipotentielle par un point donné. La circulation élémentaire sur une équipotentielle s'exprime , avec appartenant à l'équipotentielle: or U = Cte sur l'équipotentielle donc dU=0.   La circulation d'un champ dérivant d'un potentiel est nulle sur une équipotentielle. Conséquences : Puisque , cela impose que est perpendiculaire à : Le vecteur champ est partout perpendiculaire aux équipotentielles. Les lignes de champ sont les trajectoires orthogonales des surfaces équipotentielles.     3.3.4. 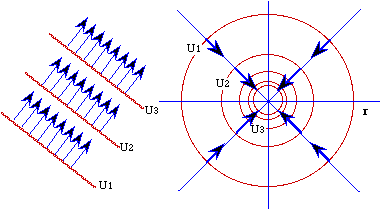Exemples de champs Champ uniforme (a): On dit d'un champ qu'il est uniforme lorsqu'il a même intensité, même direction et même sens en tous les points de l'espace. Les lignes d'un champ uniforme sont des droites parallèles au vecteur champ; ses équipotentielles sont des plans parallèles, perpendiculaires à ces droites, équidistants. Dans une zone de petites dimensions le champ de pesanteur terrestre peut être considéré comme uniforme.   (a)                                    (b) Champ central (b): Un champ est central lorsque tous les vecteurs champ passent par un même point O de l'espace. Si ce champ dérive d'un potentiel, son intensité en M ne dépend que de la distance et non de . Les équipotentielles sont des sphères de centre O. Le champ de gravitation créé par une masse ponctuelle est central

Mécanique. Champs de vecteurs - Potentiel. 3