|
 A.3.Accélération du
mobile par rapport à un référentiel A.3.Accélération du
mobile par rapport à un référentiel
Définition
Unité
Accélération normale
et accélération tangentielle
Mouvement uniforme
 A.3.1.
Définition A.3.1.
Définition
Soit 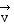 le
vecteur vitesse de M à l'instant t et le
vecteur vitesse de M à l'instant t et 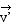 en
M' à l'instant t'. en
M' à l'instant t'.
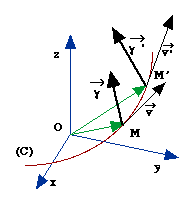
Par définition on
appelle vecteur accélération du mobile M dans le
référentiel¸
[R] le vecteur :
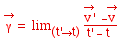
Par définition cette
limite est la dérivée du vecteur vitesse par rapport au
temps, c'est à dire aussi la dérivée seconde du
rayon vecteur ; l'application du mouvement doit donc être deux
fois dérivable par rapport au temps :
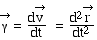
 A.3.2.
Unité. A.3.2.
Unité.
Du point de vue dimension une accélération est
le rapport d'une vitesse à un temps
[g]
=VT -1= LT -1 T -1
= LT -2
Dans le système SI, une accélération se mesure
en mètre par seconde carré ( ms-2).
 A.3.3. Accélération normale et accélération
tangentielle A.3.3. Accélération normale et accélération
tangentielle
Nous venons de voir que : 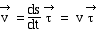
Dérivons pour obtenir l'accélération:
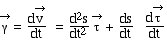
Or :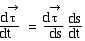 donc
donc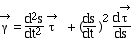
Il nous reste à déterminer 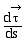
Le vecteur 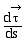 est
la limite lorsque DsÆ
0 de est
la limite lorsque DsÆ
0 de 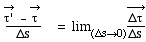
Mais 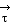 est
obtenu à partir de la limite de est
obtenu à partir de la limite de 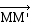 et et
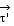 à partir de la limite de
à partir de la limite de 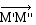 . .
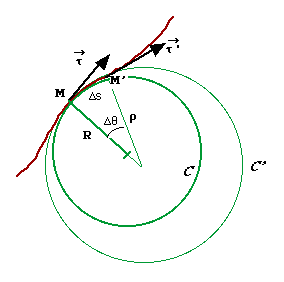
Considérons le cercle C'
de rayon r
passant par M, M'.
A l'arc Ds
correspond l'angle Dq
tel que Ds= r.Dq
On peut écrire : 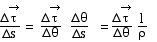
pour DsÆ
0, rÆ
R le cercle C' tend vers le
cercle osculateur C de rayon R,
d'où :
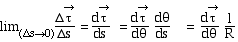
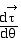 est
la dérivée d'un vecteur unitaire tangent à un cercle,
par rapport à l'angle qui détermine sa position. C'est
le vecteur normal est
la dérivée d'un vecteur unitaire tangent à un cercle,
par rapport à l'angle qui détermine sa position. C'est
le vecteur normal 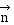 .
Par suite: .
Par suite:
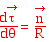
On a donc :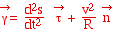 avec
avec 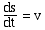 et
et 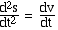
Le vecteur accélération se décompose
en :
- une
accélération tangentielle 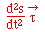 de
même direction que la vitesse (mais pas forcément de même
sens, suivant le signe de la dérivée seconde) de
même direction que la vitesse (mais pas forcément de même
sens, suivant le signe de la dérivée seconde)
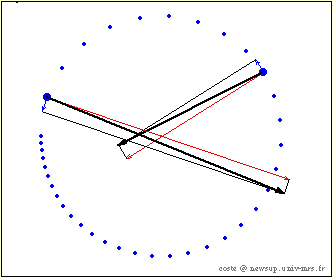
La simulation suivante montre l'accélération
tangentielle d'un mouvement circulaire non uniforme
 |
Mouvement circulaire
non uniforme
Accélération tangentielle
|
- une accélération
normale 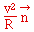 dirigée
vers le centre de courbure de la trajectoire. dirigée
vers le centre de courbure de la trajectoire.
L'accélération
tangentielle est liée à la variation de v (dérivée
de l'abscisse curviligne) et l'accélération normale à
la vitesse devariation de la direction du vecteur vitesse .
La simulation suivante montre
l'accélération normale d'un mouvement circulaire non uniforme
 |
Mouvement circulaire
non uniforme - Accélération normale
|
Par exemple, l'indicateur de vitesse d'une voiture
donne la valeur instantanée de la vitesse (c'est-à-dire la
"vitesse horaire"; dérivée par rapport au temps
de l'abscisse curviligne).
L'étude des variations de cette vitesse horaire ne pourra donner
que l'accélération tangentielle. L'accélération
normale est liée non seulement à la vitesse horaire, mais
aussi à la courbure de la trajectoire (qui n'est pas enregistrée
par le compteur).
Faire l'exercice suivant:
 Grandeurs
cinématiques dans le plan Grandeurs
cinématiques dans le plan
 A.3.4. Mouvement uniforme A.3.4. Mouvement uniforme
Par définition un
mouvement est dit uniforme
si son équation horaire est linéaire : s
= at +b , donc si sa vitesse horaire a est constante.
En conséquence, dans un mouvement curviligne uniforme
l'accélération tangentielle dv/dt est nulle, mais pas en général
l'accélération normale, sauf si la trajectoire est rectiligne.
Faire les exercices
 Mouvement rectiligne
uniforme Mouvement rectiligne
uniforme
 Mouvement uniforme Mouvement uniforme
 Mouvement circulaire
uniforme: vitesse Mouvement circulaire
uniforme: vitesse
 Mouvement circulaire uniforme : hodographe Mouvement circulaire uniforme : hodographe
 Mouvement circulaire uniforme : accélération
Mouvement circulaire uniforme : accélération
 Hodographe d'un mouvement circulaire uniforme
Hodographe d'un mouvement circulaire uniforme
|
