Mécanique - Chapitre B - 4

B.4. Expression des vitesses Composition des vitesses Vitesse d'entrainement      Roue sur un rail      Translation circulaire      Rotation sur un cercle  B.4.1. Composition des vitesses   Ayant maintenant établi la relation entre les dérivées d'un même vecteur dans deux référentiels mobiles l'un par rapport à l'autre; nous pouvons reprendre l'expression 2-2 de composition des mouvements: Nous savons maintenant écrire: Pour alléger l'écriture; nous poserons: La règle de composition des vitesses s'écrit alors :  B.4.2. 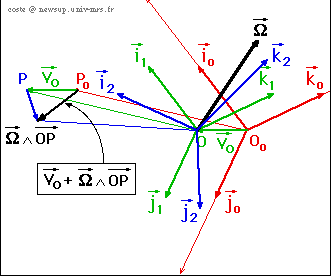Vitesse d'entrainement Par définition on appelle vitesse d'entraînement le vecteur : C'est la vitesse de P*: point coïncidant au point P à l'instant t, appartenant au référentiel en mouvement qui entraîne la particule. Cette vitesse est, dans le cas le plus général, somme d'un terme de translation et d'un terme de rotation  . Il faut noter que, à un instant donné, la vitesse d'entraînement n'est pas la même en différents points du référentiel, sauf si [R] ne tourne pas par rapport à [Ra]. La simulation suivante montre la construction de la forme la plus générale de la vitesse d'entraînement. 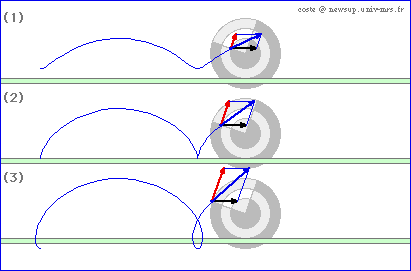Vitesse d'entraînement La simulation suivante montre la construction de la vitesse résultante de la composition d'un mouvement d'entraînement rectiligne uniforme (référentiel noir) et d'un mouvement circulaire uniforme (référentiel rouge). Roue sur rail Dans la simulation suivante, le référentiel VERT est en translation circulaire par rapport au référentiel (R). La vitesse d'entrainement est la même pour tous les points du référentiel VERT Translation circulaire     Par contre, dans la simulation ci-dessous,le référentiel VERT est en rotation par rapport au référentiel (R).La vitesse d'entrainement dépend de la position du point du référentiel VERT Rotation sur un cercle     Faire l'exercice suivant: Vitesse de libération

Mécanique - Chapitre B - 4