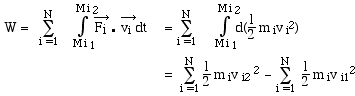|
 F.2. Théorème
de l'énergie cinétique F.2. Théorème
de l'énergie cinétique
Cas du point matériel
Cas d'un système
de points matériels.
Expression instantanée
du théorème de l'énergie cinétique
Unité d'énergie
cinétique.
 F.2.1.
Cas du point matériel. F.2.1.
Cas du point matériel.
Nous supposons maintenant le référentiel
[R] galiléen et un point matériel mobile M de masse m animé
d' une vitesse instantanée 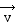 dans [R] et auquel est appliquée
une force dans [R] et auquel est appliquée
une force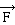 . .
Le théorème de la quantité de
mouvement appliqué à M s' écrit :
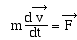
Le travail de la force au cours du déplacement
du mobile de M1 à M2 est:
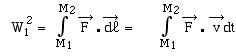
Compte tenu de l' expression du principe fondamental
ci-dessus:
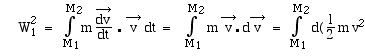 ) )
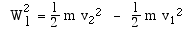
en appelant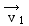 la vitesse du mobile en M1
et la vitesse du mobile en M1
et 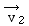 sa vitesse en M2. sa vitesse en M2.
|

|
Théorème de l' Energie
cinétique pour un point:
La variation de l' énergie cinétique d' un point matériel lorsqu'
il parcourt sa trajectoire d' un point M1 à un point M2
est égale au travail de la résultante des forces appliquées
au point matériel de M1 à M2 le long de la trajectoire. |
Remarque :
On a dit "travail de la résultante des
forces" car ces forces sont toutes appliquées au même point M et
on se trouve dans le cas où le travail de toutes les forces est égal
au travail de la résultante.

La simulation suivante montre la chute
de deux corps à laquelle peut s'appliquer le théorème précédent.
Dans le cas de gauche, on considère que la seule force agissant sur la boule
est son poids. Dans le cas de droite, en plus du poids de la balle agit une force
de résistance de l'air.
|

|
Travail des forces
|
Faire les exercices:
 Looping Looping
 Distance de freinage Distance de freinage
 Exprimer l'énergie cinétique. Exprimer l'énergie cinétique.
 Exprimer l'énergie cinétique Exprimer l'énergie cinétique
 F.2.2. Cas d'un système de points
matériels. F.2.2. Cas d'un système de points
matériels.
Soit un système de N points matériels
dans un référentiel [R] galiléen le point Mi de masse
mi est animé à l' instant t d' une vitesse 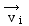 et est soumis
à l' action d' une force et est soumis
à l' action d' une force 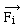 qui se décompose
naturellement en qui se décompose
naturellement en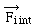 (force intérieure) et (force intérieure) et  (force extérieure
au système). (force extérieure
au système).
Dans [R] galiléen, le théorème
de la quantité de mouvement appliqué à Mi s' écrit:
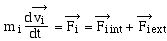
Envisageons un déplacement du système;
le déplacement d' un point Mi est en général différent
de celui d' un autre point M.
Pour le point Mi : appelons Mi1 le point de
départ et Mi2 le point d' arrivée sur la trajectoire suivie par Mi
Le travail de la force s' écrit : 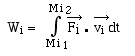 et pour tous
les points matériels du système, on fait la somme des travaux de toutes
les forces: et pour tous
les points matériels du système, on fait la somme des travaux de toutes
les forces:
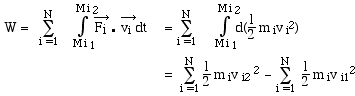
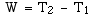
Il faut bien remarquer que:

|

|
Théorème de l' Energie
cinétique pour un système:
Dans un référentiel galiléen, la variation d' énergie
cinétique d' un système de points matériels entre un instant
de départ et un instant d' arrivée est égale à la somme
des travaux de toutes les forces (intérieures et extérieures) appliquées
à chacun des points du système le long de la trajectoire de chacun
de ces points dans le même intervalle de temps |
Remarque:
Le théorème de l' énergie cinétique
n' a de sens que si le référentiel par rapport auquel on détermine
cette énergie cinétique est galiléen.
 F.2.3.
Expression instantanée du théorème de l'énergie cinétique F.2.3.
Expression instantanée du théorème de l'énergie cinétique
Considérons une force appliquée
en un point M décrivant une trajectoire (C) avec une vitesse instantanée
dans un référentiel [R].
La puissance instantanée de la force 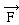 dont le point
d' application se déplace avec une vitesse instantanée dans le référentiel
R est la grandeur scalaire: dont le point
d' application se déplace avec une vitesse instantanée dans le référentiel
R est la grandeur scalaire:
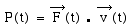
Or, à tout instant, on a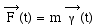 et en reportant dans l' expression de la puissance,
on obtient :
et en reportant dans l' expression de la puissance,
on obtient :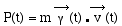 qui n' est pas autre chose que la dérivée
par rapport au temps de la fonction T : énergie cinétique": qui n' est pas autre chose que la dérivée
par rapport au temps de la fonction T : énergie cinétique":
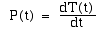
|

|
Dans le mouvement d' un point matériel
par rapport à un référentiel galiléen, la puissance de
la force totale est la dérivée par rapport au temps de l' énergie
cinétique du point. |
 F.2.4.
Unité d'énergie cinétique. F.2.4.
Unité d'énergie cinétique.
Il résulte du théorème de
l' énergie cinétique que l' énergie cinétique a même
dimension qu' un travail.
Dans le système SI, l' énergie cinétique
s' exprime comme le travail en Joule.
|
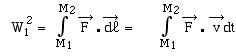
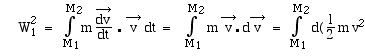 )
)

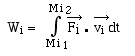 et pour tous
les points matériels du système, on fait la somme des travaux de toutes
les forces:
et pour tous
les points matériels du système, on fait la somme des travaux de toutes
les forces: