Sous-espaces supplémentaires

Définition

Définitions 1) Deux sous-espaces vectoriels F et G d'un K-espace vectoriel E sont des sous-espaces vectoriels supplémentaires de E si leur somme est directe et est égale à l'espace vectoriel E tout entier : 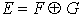   2) Si F et G sont des sous-espaces vectoriels supplémentaires du K-espace vectoriel E, on dit que F est un supplémentaire de G, ou que G est un supplémentaire de F.

et donc d'après ce qui précède :

Propriétés caractéristiques Deux sous-espaces vectoriels F et G d'un K-espace vectoriel E sont des sous-espaces vectoriels supplémentaires de E si et seulement si tout élément de E s'écrit d'une manière unique comme la somme d'un élément de F et d'un élément de G. Deux sous-espaces vectoriels F et G d'un K-espace vectoriel E sont des sous-espaces vectoriels supplémentaires de E si et seulement si et .

	L'existence d'un supplémentaire d'un sous-espace vectoriel est prouvée dans le cadre des espaces vectoriels de type fini.
	Il n'y a pas unicité du supplémentaire d'un sous-espace vectoriel donné (voir exemple suivant).

   Exemple :

L'espace vectoriel R² est la somme directe du sous-espace vectoriel F engendré par (1,0) et du sous-espace G engendré par (0,1), donc F et G sont des sous-espaces vectoriels supplémentaires de R².
Mais l'espace vectoriel R² est aussi la somme directe du sous-espace vectoriel F engendré par (1,0) et du sous-espace vectoriel H engendré par (1,1), donc F et H sont aussi des sous-espaces supplémentaires de R².

 Cliquez moi pour voir la preuve !

Sous-espaces supplémentaires