Démonstration par récurrence en supposant comme hypothèse de récurrence la propriété vraie pour tous les déterminants d’ordre inférieur à n.

Le déterminant s’annule si deux des vecteurs V_i et V_j sont égaux pour des indices i 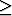 2 et j  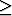2. Ce cas est facile à démontrer par récurrence en utilisant la définition pour tous les déterminants d’ordre
n - 1.

Le déterminant s’annule si deux des vecteurs V₁ et V_j sont égaux pour un indice j 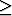 2. Ce cas est moins facile à démontrer par récurrence. Il faut de nouveau développer tous les déterminants D_i1 par rapport à la première colonne en utilisant la propriété pour tous les déterminants d’ordre n - 1. Soient D_kl le déterminant obtenu en barrant les colonnes 1 et i et les lignes k et l. Ces déterminants apparaissent quand on développe le déterminant initial suivant la première colonne, puis les sous-déterminants suivant la colonne issue du vecteur V_i . Dans les sommes issues de ces calculs, D_kl apparaît deux fois avec des coefficients opposés :
a_k1a_li et - a_kia_l1 , (on n’oublie pas que les colonnes 1 et i sont identiques). On obtient une somme de n(n - 1) termes et donc un nombre pair de termes. Ceux-ci se regroupent deux à deux. Donc la somme est nulle.

On démontre la propriété d’antisymétrie en utilisant la propriété précédente, det(V₁, V₂, V₃, ..., V_n) = 0 si deux colonnes sont égales et la bilinéarité et en développant le déterminant