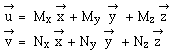 |
Mécanique. Représentation de l'espace.5 |
 |
|
Le produit scalaire est une application de E
x E sur R qui fait correspondre au couple
Dans l'espace vectoriel Euclidien
E, on définit le produit scalaire
On définit une norme associée au produit scalaire à l'aide de la racine carrée du produit scalaire d'un vecteur par lui-même.
On montre en mathématiques que, pour une origine
prise au point O,
Ceci nécessite d'avoir défini :
Remarques: a) La définition
intrinsèque est à relier à la propriété
de définition : b) La définition intrinsèque permet de définir l'orthogonalité :
Si les vecteurs On introduit ainsi la notion de base orthonormée où tous les vecteurs de base sont orthogonaux 2 à 2 et où la norme de chaque vecteur de base est égale à l'unité.
Elle nécessite d'exprimer les vecteurs et sur
une base. Soit
On peut alors exprimer : Le produit scalaire s'obtient en utilisant la propriété de bilinéarité, soit en développant le calcul : Pour terminer le calcul il faut connaître non seulement les composantes mais les produits scalaires qu'on peut faire avec les vecteurs de la base pris deux à deux. Le cas le plus simple est celui d'une base orthonormée. |
1.5.
Produit scalaire
.
Cette application possède les propriétés suivantes:
des
deux vecteurs 
:
ou
encore 
entre les vecteurs 
.
En effet :
une base dans laquelle les vecteurs sont représentés par
leurs composantes, soit : 
dont les composantes sont (Mx,
My ,
Mz)
dont les composantes sont (Nx,
Ny ,
Nz).
