La chute de pression (ou perte de charge) subie par un liquide à la traversée d'une longueur Z de milieu poreux peut être calculée, si le régime d'écoulement est laminaire, par la loi de KOZENY.

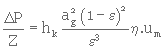
ε est la porosité du milieu.

ε est un nombre sans dimension compris entre 0 et 1

a est l'aire spécifique de grain, c'est l'aire de la surface en contact avec le liquide correspondant à un volume unité de solide.

Si le volume de solide constituant le milieu poreux est V_g et si la surface de contact correspondante est A_g , l'aire spécifique est :

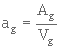
L'aire spécifique a pour dimension :

[a_g] = L^-1

Il est important de remarquer que plus une poudre est fine et plus son aire spécifique est importante.

Un milieu poreux n'est pas nécessairement constitué de grains, dans ce cas, on utilisera l'aire spécifique de couche a c.

On peut vérifier la relation entre l'aire spécifique de couche et l'aire spécifique de grain.

a_c = a_g (1-ε)

h_k est la constante de KOZENY, c'est un nombre sans dimension déterminé de façon expérimentale et qui tient compte de la forme sinueuse et mal définie des pores (voir paragraphe sur le modèle de KOZENY).

Lorsque la porosité est inférieure à 0,6, la constante de KOZENY ne varie pas beaucoup avec la forme des grains, on peut admettre :

h_k = ±1

Par contre, dans les garnissages (anneaux RASCHIG, selles de BERL, etc...) la porosité est très forte et la constante de KOZENY varie d'un garnissage à l'autre. Elle prend des valeurs supérieures à 10.

En résumé, la porosité e, l'aire spécifique de grain ou de couches, la constante de KOZENY sont trois caractéristiques du milieu poreux. Bien que souvent difficile à déterminer, elles permettent de prévoir la valeur de la perméabilité d'un milieu poreux. En comparant la loi de DARCY

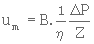
et la loi de KOZENY

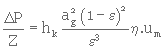
on obtient l'expression de la perméabilité :

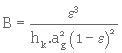
Remarque 1 :

Lorsque la forme des grains ne s'éloigne pas trop de la forme sphérique, on peut définir leur dimension par une seule grandeur que l'on appellera souvent diamètre d g. Si cette dimension ne varie pas beaucoup d'un grain à un autre, on pourra par approximation définir un diamètre moyen de grain d g et calculer

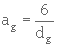
Dans ces conditions :

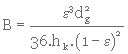
L'intérêt de cette relation est de montrer qu'en gros, la perméabilité augmente comme le carré de la dimension des grains constituant le milieu poreux. Comme 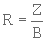, à épaisseur égale, un milieu poreux constitué de grains 10 fois plus petits qu'un autre, présentera une résistance à l'écoulement 100 fois plus grande. Autrement dit, pour assurer le même débit, il faudra que la pression amont soit 100 fois plus forte.

Remarque 2 : Modèle de KOZENY

La loi de KOZENY est obtenue à partir d'une représentation fictive des milieux poreux.

Cette représentation appelée MODELE DE KOZENY consiste à remplacer le milieu poreux réel par un milieu de même volume apparent traversé par des capillaires non interconnectés de section circulaire de diamètre dp et de longueur Zp supérieure à Z. Le nombre de capillaires par unité de volume apparent de milieu poreux est Np . Les valeurs de Np et de dp sont choisies de telle sorte que la surface totale des capillaires soit égale à l'aire spécifique de couche et que le volume total des capillaires soit égal au volume poreux.

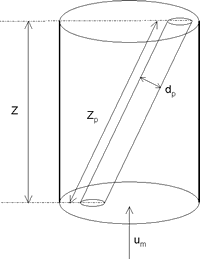Dans ces conditions, on montre que :

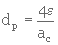
et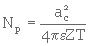

où 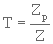est la tortuosité

La tortuosité T n'est pas un nombre arbitraire, elle correspond à la longueur "moyenne" parcourue par le fluide dans les pores réels.

La loi de KOZENY peut être considérée comme une loi semi-empirique, elle applique une loi théorique (la loi de POISEUILLE) à un modèle arbitraire et n'ayant que très peu de rapport avec la réalité (le modèle de KOZENY). Il est important de noter que ce modèle n'a de justification que parce qu'expérimentalement il permet de rendre compte avec une précision suffisante de l'écoulement dans de nombreux milieux poreux.

La loi de KOZENY dérivée de la loi de POISEUILLE ne peut donc être vérifiée qu'en régime d'écoulement laminaire.

Par suite de la variation de h_k avec la porosité lorsque e est supérieure à 0,6, la loi de KOZENY n'est utile qu'en dessous de cette valeur.