La particule est soumise à une force :

F = Q E (4. 20)

avec

• E champ électrique en (V/m),
• Q charge (en C), égale au nombre de charges élémentaires multiplié par la charge d'un électron.

La vitesse de migration sera, comme dans le cas de la gravitation, calculée en équilibrant la force découlant de la loi de Stokes à cette force électrique :

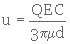(4. 21)

avec C coefficient de traînée.

Les électrofiltres pouvant capturer des particules submicroniques, le coefficient de traînée sera calculé en appliquant la correction de Cunningham. Le mécanisme global est décrit par le schéma de la Figure 4. 26 .

Pendant qu'elles sont attirées vers la contre-électrode, les particules sont aussi poussées par le gaz, ce qui fait que l'électrofiltre ne dispose que d'un temps limité pour exercer son action. Si l'on suppose que les particules collectées à la paroi ne peuvent pas être entraînées, on aboutit à la relation de Deutsch qui donne l'efficacité du procédé en fonction de la vitesse de migration des particules et du débit gazeux :

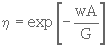(4. 22)

avec

• w : vitesse de migration,
• A : surface offerte par les contre-électrodes,
• G : débit gazeux.

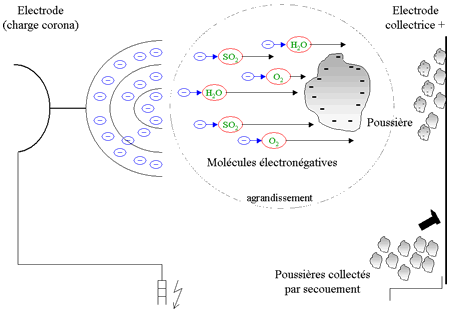
Figure 4. 26  : mécanisme de charge et de déplacement des particules dans le champs électrique

Il faut bien insister sur le caractère théorique de cette loi, qui est de peu d'utilité dans l'absolu. Néanmoins cette loi est précieuse car une fois w déterminé empiriquement par déduction à partir d'un point de fonctionnement, elle permettra de dire ce qu'il en adviendra du rendement à la suite d'une variation du débit à traiter. Une courbe d'efficacité type est représentée sur la Figure 4. 27 . Elle passe par un minimum caractéristique de beaucoup de procédés. Aux très faibles tailles de particules, les mécanismes diffusionnels prennent une importance considérable et l'efficacité est augmentée. Une fois arrivées à la surface de collecte, les particules vont constituer un dépôt plus ou moins cohérent qui devra être éliminé.

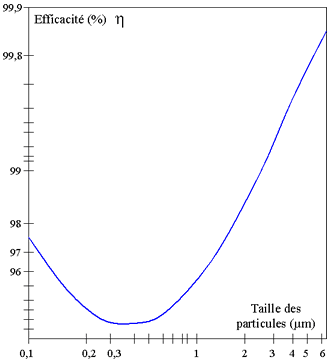
Figure 4. 27  : efficacité d'un électrofiltre en fonction de la taille des particules

Le procédé le plus courant consiste à frapper les plaques de manière périodique avec de gros marteaux. Des vibrations sonores peuvent aussi être employées.

Les installations industrielles (Figure 4. 24) sont généralement encombrantes et d'un coût assez élevé.