Cas d'un décanteur statique à flux horizontal

Considérons un bassin rectangulaire, de surface S et de profondeur H, à écoulement horizontal continu. Nous y distinguerons quatre zones :

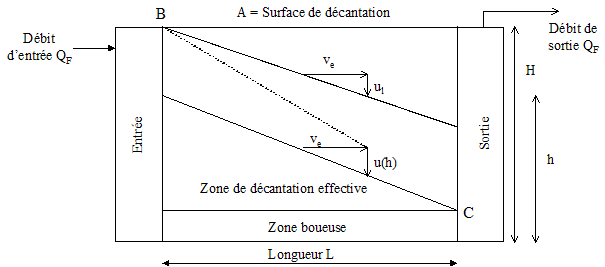
Figure 1. 6: décanteur statique à flux horizontal

• une zone d'alimentation (entrée) à travers laquelle on suppose que le débit d'entrée Q est uniformément distribué,
• une zone de sédimentation où s'effectue la chute des particules individuelles,
• une zone boueuse sous-jacente, où s'accumulent les matières sédimentées,
• une zone de sortie.

La trajectoire de la particule est rectiligne, elle correspond à la résultante de deux déplacements :

• un déplacement d’ensemble horizontal à la vitesse v_e
• un déplacement individuel vertical à la vitesse de sédimentation u_l

Pour un bassin de longueur L, de largeur l, et de hauteur H nous avons :

v_e = 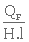(1. 17)

Pour qu'une particule sédimente c’est à dire pour qu’elle soit arrêtée au fond du décanteur, sa trajectoire doit être plus inclinée que la diagonale BC soit :

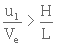(1. 18)

d’où : u_l >

soit : u_l > 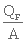(1. 19)

avec A = L .l

Les particules entrant dans la zone de décantation effective avec une vitesse de chute u(h) plus faible que la vitesse de chute limite u_l et peuvent sédimenter si elles entrent à une hauteur h inférieure à la hauteur du décanteur H.

u(h) = u_l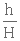 (1. 20)

Le rendement de séparation de la classe de particules de vitesse u(h) et le rendement global de séparation, dans le cas d'une suspension de particules de tailles diverses, dépendront donc de la surface du bassin, et non de son volume. Le calcul des performances de l’appareil traitant une suspension donnée, consistera donc :

• à définir un ensemble de classes de particules se caractérisant chacune par une vitesse de sédimentation moyenne,
• à calculer le pourcentage retenu pour chaque classe et
• à totaliser ces valeurs pour obtenir le rendement global.

La méthode la plus rapide consiste à recourir à une intégration graphique à partir de la courbe de distribution cumulée des vitesses de sédimentation. La démarche sera inverse si le débit d’effluent et le rendement de séparation sont imposés et que l'on veut dimensionner le décanteur.
Dans le cas particulier où l'introduction de la suspension se fait dans la partie supérieure du bassin au lieu d'être répartie dans toute la section, seules les particules ayant une vitesse de sédimentation supérieure à ul seront retenues.

Cas d'un décanteur statique à flux vertical

Soit A la surface du bassin et Q_F le débit d'alimentation en suspension peu concentrée. La vitesse ascensionnelle du liquide est :

u = 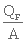(1. 21)

Pour clarifier la suspension, il faut que cette vitesse soit inférieure à la vitesse de chute u_l de la plus petite particule à retenir. La surface minimale du décanteur sera donc :

A = 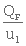(1. 22)

Une installation caractéristique de ce type est représentée ci-après. Il s'agit du décanteur statique cylindro-conique ordinaire. Dans cet appareil l'eau de débit Q_F subit, après une répartition convenable, un mouvement ascendant dans toute la section S du décanteur. Le rapport, appelé vitesse ascensionnelle, est le paramètre fondamental de l'exploitation. Toutes les particules ayant une vitesse inférieure à u_l seront entraînées hors du décanteur, les autres étant retenues et se concentrant sous forme de boues à la base de l’appareil.

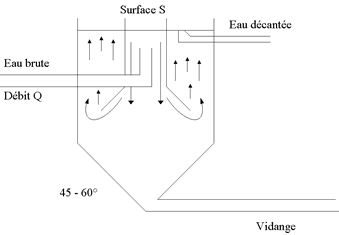
Figure 1. 7 : Schéma d’un décanteur cylindro-conique

Photo 1. 1 : Décanteur cylindro-conique