Nous avons vu qu'une particule atteint sa vitesse terminale de chute lorsque la traînée, correspondant à la vitesse de la particule, est égale à son poids apparent.

Le poids apparent d'un grain sphérique est égal au poids du grain diminué de la poussée d'Archimède P - PA. Un grain sphérique de diamètre d_g a pour volume :

V_g = 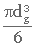(1. 9)

Si la masse volumique du grain est ρ_s, le poids du grain est :

P = V_gρ_sg (1. 10)

ou encore, en utilisant l'équation 1. 9 :

P = 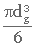ρ_sg (1. 11)

La poussée d'Archimède dans un fluide de masse volumique est :

P_A = 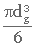ρ_lg (1. 12)

La vitesse terminale de chute u_l est la vitesse pour laquelle la traînée atteint sa valeur limite c'est à dire F_T(u_l) = P - PA

• Si u_l correspond au régime de STOKES on aura :

u_l = (1. 13)

Avec Re_g = < 1



• Si u_l correspond au régime intermédiaire d'ALLEN, elle sera calculée par la relation :

u_l = (1. 14)

avec 1<Reg<1000



• Si u_l correspond au régime de NEWTON, on aura :

  F_T(u_l) = 0,055πρ_ld_g²u₁² = (ρ_s-ρ_l)g (1. 15)
  
  soit : u_l = (1. 16)
  
  avec 10³ < Reg < 4.10⁵
  

Cas des particules non sphériques

Il est rare que les matières en suspension contenues dans l'eau soient sphériques. A volume égal, les particules non sphériques présentent une surface développée plus grande que les particules sphériques. De ce fait, la vitesse de chute est plus faible et peut être calculée, pour un type déterminé de particules, par application d'un facteur de forme adéquat.