Lois fondamentales

De nombreux travaux ont été effectués pour décrire mathématiquement la sédimentation freinée. Les théories actuelles dérivent de celle de KYNCH , qui a formulé l'hypothèse de base suivante :

La vitesse de chute d'une particule, quelles que soient sa taille et sa densité, dépend uniquement de la concentration locale en particules de la zone qu'elle traverse, et décroît lorsque la concentration augmente.

Cette hypothèse permet d'expliquer l'allure de la portion BCD de la courbe ci-dessus et de montrer que, contrairement aux apparences, la partie linéaire BC et la partie incurvée CD sont régies par la même loi fondamentale.

A l'instant initial t₀ , la suspension est homogène, de concentration C₀ , et par conséquent toutes les particules vont se déplacer avec une vitesse identique v₀ .

Au bout d'un temps très court t₁ , il va se créer au fond du tube une augmentation de la concentration locale, qui deviendra C₁ . Les particules entrant dans cette zone vont se déplacer à une vitesse v₁ inférieure à v₀ , tandis que toutes celles qui se trouvent au-dessus continueront à se mouvoir à la vitesse v₀.

Au temps t₂ , la zone de concentration C₁ se sera déplacée vers le haut. Au-dessus de cette zone, la vitesse des particules et, par conséquent, de l'interface, sera toujours v₀ , elle sera de v₁ dans la zone de concentration C₁ , et sera inférieure à v₁ dans les zones de plus fortes concentrations qui se trouvent au-dessous de C₁ .

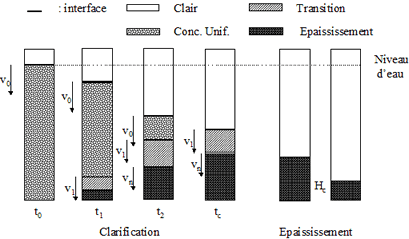
Figure 1. 22 : diverses phases de décantation d'une suspension concentrée

Au temps t_c , la zone de concentration C₁ , qui est animée d'un mouvement fictif ascendant, rencontrera l'interface qui se déplace vers le bas. A ce moment, la vitesse de chute de l'interface deviendra v₁< v₀. Sur la figure h=f(t), l'interface se trouve alors à la position correspondant au point C. La partie linéaire de la courbe est terminée.

Au point t₃ (t_C< t₃< t_D ), c'est une zone de concentration supérieure à C₁ qui atteint l'interface, cette dernière se déplace à une vitesse inférieure à v₁. Pour des durées de décantation comprises entre t_C et t_D , la vitesse de l'interface diminuera constamment, ce qui correspond à la partie incurvée CD de la courbe.

Enfin, à l'instant t_D , la loi de déplacement de l'interface ne sera plus prévisible par la loi de KYNCH , un nouveau phénomène étant impliqué : la compression du sédiment.

L'hypothèse fondamentale de KYNCH a pu être vérifiée expérimentalement, et même explicitée dans certains cas où on a pu montrer que la relation entre la vitesse de chute v de l'interface et la concentration locale C en particules est de la forme :

 

Calcul d'un décanteur en régime de sédimentation freinée

Le calcul se fait par exploitation de la courbe de sédimentation freinée tracée au cours d'un essai discontinu en colonne.

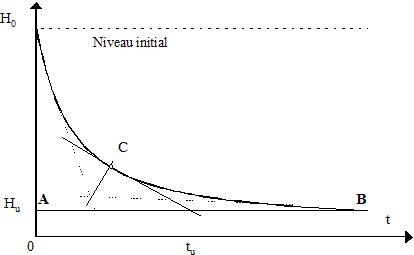
Figure 1. 23  : construction graphique pour le calcul d'un décanteur en régime de sédimentation freinée

Connaissant le débit Q et la concentration C₀ de la suspension à l'entrée, le problème consiste à déterminer la surface A de l'ouvrage nécessaire pour pouvoir extraire une boue ayant la concentration C_u que l'on se fixe, tout en ayant un liquide surnageant clarifié. La profondeur H étant fixée a priori, ce problème admet une résolution graphique (Figure 1. 23).

On détermine tout d'abord la hauteur de l'interface H_u correspondent à la concentration C_u. La conservation de la quantité de matières en suspension au cours de la décantation, nous permet d'écrire :

C₀ H₀ A=C_u H_u A

d'où :

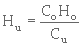
Puis on trace une droite horizontale AB, passant par le point d'abscisse nulle et d'ordonnée H_u . On détermine d'autre part le point de compression C, placé à l'intersection de la courbe de sédimentation et de la bissectrice de l'angle des tangentes qui lui sont menées aux parties initiale et finale. L'intersection de AB et de la tangente menée en C à la courbe de sédimentation a pour abscisse la durée nécessaire t_u pour obtenir la concentration C_u . La surface de l'ouvrage sera donc égale à :

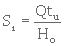(1. 25)

Il faut d'autre part que la vitesse ascensionnelle dans le décanteur soit inférieure à la vitesse v₀ de chute de l'interface, calculée à partir de la partie linéaire de la courbe de sédimentation. La surface nécessaire pour satisfaire à cette condition sera :

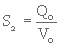(1. 26)

où Q₀ est le débit de trop-plein, c'est-à-dire la différence entre le débit entrant et celui d'extraction des boues. Il est proportionnel au volume occupé par le liquide surnageant au temps t_u , donc égale à :

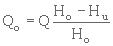(1. 27)

En pratique, on prendra comme surface du décanteur la plus grande des valeurs trouvées pour S₁ et S₂.