Bien entendu, on doit considérer en premier lieu les caractéristiques intrinsèques du matériau ou de la substance dont les solides sont constitués. Pour l'épuration des gaz, la masse volumique réelle de la particule est d'une importance particulière puisque dépend d'elle la réponse inertielle aux forces qui seront éventuellement appliquées. La plupart des applications industrielles engendrent des particules de masse volumique comprise entre 1 000 et 3 000 kg/m³. La dureté et le caractère abrasif et érosif sont également importants. Mais le facteur le plus important reste la taille, associée à la distribution granulométrique (PSD, Particle Size Distribution).

1- Taille des particules : La définition de la taille est aisée et unique quand la particule est sphérique. Mais, dès lors qu'elle ne l'est plus, on a le choix entre travailler avec plusieurs paramètres, ce qui est incommode, et travailler avec une donnée moyenne unique pour une particule. On peut prendre, par exemple, un diamètre recalculé à partir de la masse de la particule supposée shérique. On a alors :

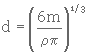(4. 6)

Le Tableau 4. 2 donne quelques-uns des diamètres équivalents les plus employés. On peut également donner une valeur à l'aide du nombre de Mesh.

Tableau 4. 2  : diamètres équivalents les plus employés pour les particules solides

Type	Définition
Diamètre de Sauter	Diamètre d'une sphère ayant le même rapport surface/volume
Diamètre surfacique	Diamètre d'une sphère ayant la même surface
Diamètre volumique	Diamètre d'une sphère ayant le même volume
Diamètre de Stokes	Diamètre d'une sphère ayant la même vitesse de chute

2- En plus de son diamètre, une particule est caractérisée par sa forme. Ainsi elle peut être en aiguille, oblongue, sphérique, filamenteuse, en écaille aplatie, voire même franchement irrégulière. On peut à nouveau tenter de qualifier ces formes par différents paramètres seulement ceux-ci, n'ont pratiquement aucun intérêt du point de vue du dépoussiérage.

3- Une question plus importante concerne le diamètre moyen d'une population. À nouveau, on a le choix entre pondérer par la longueur (diamètre), la surface, ou le volume. Le diamètre moyen le plus utilisé reste cependant celui de Sauter calculé comme suit :

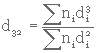(4. 7)

4- Une information plus globale est donnée par la distribution granulométrique.

Les distributions de particules les plus utilisées pour décrire mathématiquement une répartition sont :

• la distribution normale :

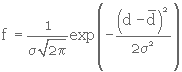(4. 8)

avec

• σ écart-type,
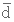• diamètre moyen.

L'adéquation de cette distribution est douteuse, dans la plupart des cas ;

• la distribution log-normale qui est une distribution normale avec des échelles logarithmiques ;
  
  
• et la distribution de Rosin/Rammler, la plus utilisée, et donnée par :

f = 100nbd^n-1exp(-bdⁿ)

avec n et b deux constantes décrivant la distribution.

 

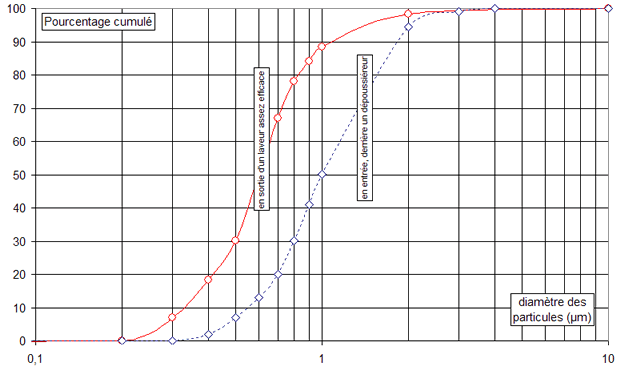
Figure 4. 2  : distribution granulométrique type

On recherchera en particulier si plusieurs modes de distribution granulométrique apparaissent, ce qui peut caractériser éventuellement une double pollution du gaz par deux solides différents, par exemple de la chaux et du charbon actif, tous deux utilisés en épuration du gaz et des fumées. Une distribution type après épuration par des laveurs est donnée par la (Figure 4. 2).