3.3.1.1. Diamètre effectif et coefficient d'uniformité
Le diamètre effectif, DE , et le coefficient d'uniformité, Cu , sont deux caractéristiques granulométriques importantes d'un matériau filtrant. Le diamètre effectif correspond à la grosseur des mailles du tamis qui laissent passer 10% de la masse de l'échantillon. Ainsi, si on connaît DE , on sait que 90 % ( en masse) des grains de l'échantillon ont un diamètre supérieur à DE . Le coefficient d'uniformité est le rapport entre le diamètre qui laisse passer 60 % des particules et celui qui en laisse passer 10 %, soit D 60 /D 10 .
Pour mesurer DE et Cu , on pèse une certaine quantité de matériau filtrant préalablement débarrassée de toute humidité, puis on place cet échantillon sur une série de tamis dont les mailles sont de plus en plus petites. Le Tableau 3. 1 présente les dimensions des ouvertures des tamis utilisés dans le système U.S. Standard et dans le système Tyler. Pour favoriser le tamisage, on fait vibrer la série de tamis; on évite cependant les vibrations violentes lorsque les grains du matériau filtrant sont friables. On pèse ensuite la quantité de matériau filtrant retenue par chaque tamis: on en déduit ainsi le pourcentage de l'échantillon qui traverse chaque tamis, donc le pourcentage des grains dont le diamètre est inférieur au diamètre des mailles du tamis. On trace ensuite, sur papier semi-logarithmique,la variation du pourcentage de l'échantillon dont les grains ont un diamètre inférieur à D (échelle arithmétique) en fonction du diamètre, D (échelle logarithmique).
Tableau 3. 1 : Ouvertures de différents tamis utilisés pour mesurer le diamètre effectif et le coefficient d'uniformité d'un matériau filtrant
Tamis |
Diamètre des particules (mm) |
| |
Système U.S. Standard |
Système Tyler |
4 po
3po
2 ½ po
2 po
1 ½ po
1 po
¾ po
½ po
3/8 po
¼ po (n°3)
n°4
n°6
n°8
n°10
n°14
n°16
n°18
n°20
n°30
n°40
n°50
n°60
n°65
n°100
n°140
n°200
n°270
n°400 |
101,6
76,2
-
50,8
-
25,4
19,1
12,7
9,52
6,35
4,76
3,35
2,38
2,00
1,40
1,19
1,00
0,84
0,59
0,42
0,297
0,25
-
0,149
0,105
0,074
0,053
0,037 |
-
76,2
-
50,8
-
26,67
18,85
13,33
9,42
6,68
4,70
-
2,36
1,651
-
1,168 (n° 14)
-
0,833
0,589 (n°28)
0,417 (n°35)
0,295 (n°48)
0,246
0,208
0,147
0,104 (n°150)
0,074
0,053
0,038 |
|
|
En utilisant la courbe ainsi obtenue, on peut alors estimer le diamètre effectif, DE , et le coefficient d'uniformité, Cu , du matériau filtrant mis à l'épreuve. C'est ce que l'Exemple 3. 1 illustre.
Exemple 3. 1
Calculer le diamètre effectif et le coefficient d'uniformité d'un sable et d'un anthracite pour lesquels les essais de tamisage ont donné les résultats présentés aux Tableau 3. 2 et Tableau 3. 3.
Tableau 3. 2 : Caractéristiques granulométriques d'un sable (exp. 3.1)
N° de Tamis
(U S Standard)
|
Diamètre des mailles (mm) |
Pourcentage de l'échantillon retenu |
Pourcentage cumulatif retenu |
Pourcentage qui traverse chaque Tamis |
16
203
30
50
100 |
1,19
0,84
0,59
0,297
0,149 |
0
14,9
50,1
33,5
1,5 |
0
14,9
65
98,5
100 |
100
85,1
35
1,5
0 |
|
Tableau 3. 3 : Caractéristiques granulométriques d'un anthracite (exp. 3.1)
N° de Tamis
(U S Standard)
|
Diamètre des mailles (mm) |
Pourcentage de l'échantillon retenu |
Pourcentage cumulatif retenu |
Pourcentage qui traverse chaque Tamis |
8
16
20
30
50
100 |
2,38
1,19
0,84
0,59
0,297
0,149 |
2,0
66,0
22,2
6,2
2,5
0,5 |
2,0
68,0
90,2
96,4
98,9
99,4 |
98,0
32,0
9,8
3,6
1,1
0,6 |
|
|
Solution
Grâce à ces données, on trace, sur papier semi-logarithmique, les courbes présentées à la Figure 3. 1, à partir desquelles on peut calculer le diamètre effectif et le coefficient d'uniformité du sable (DE = 0,47 mm et Cu = 1,55) et de l'anthracite (DE = 0,80 mm et Cu = 1,83).
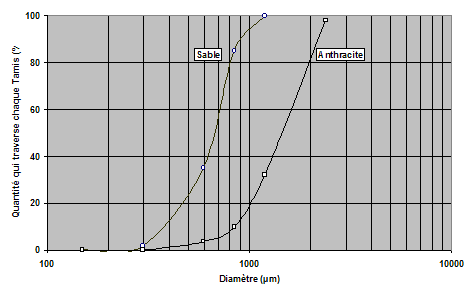
Figure 3. 1 : Courbes granulométriques d'un sable et d'un anthracite (exp. 3.1).
3.3.1.2. Densité relative du sable
On peut calculer expérimentalement la densité relative du sable, γs, en divisant sa masse par celle de l'eau qu'il déplace. On procède de la façon suivante :
- on pèse un certain volume d'eau (on obtient me) ;
- on pèse le sable sec (on obtient ms) ;
- on ajoute le sable à l'eau (l'eau déplacée déborde du récipient) ;
- on pèse le mélange d'eau et de sable ( on obtient mes).
On peut ainsi écrire :
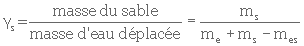(3.1)
3.3.1.3. Masse unitaire sèche
La masse unitaire sèche, ρu, est la masse de matériau filtrant par unité de volume, masse qui varie en fonction du degré de compactage du matériau. Ainsi, on peut mesurer la masse unitaire sèche minimale ou la masse unitaire sèche maximale.
Pour mesurer la masse unitaire sèche minimale, on verse le sable, dans un récipient de volume et de masse connus, selon une technique qui permet d'éviter tout compactage. On pèse ensuite le récipient plein pour déterminer la masse de sable par unité de volume.
Pour mesurer la masse unitaire sèche maximale, on fait vibrer le récipient pour obtenir un compactage maximal du sable, puis on pèse le récipient plein pour déterminer la masse de sable par unité de volume.
3.3.1.4. Porosité
On calcule la porosité, ε, d'un matériau en divisant le volume des vides dans ce matériau par le volume total du matériau.
sachant que
- vs = volume des solides
- vv = volume des vides
- vT = volume total du matériau
- ρu= masse unitaire sèche du matériau
- γs= densité relative du sable
On peut écrire
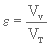(3. 2)
En supposant un volume total unitaire (vT = 1), on peut aussi écrire
ρu=vs.γs.ρ (3. 3)
et
vT = vv+ vs (3. 4)
En combinant les équations 3. 2, 3. 3 et 3. 4, on obtient
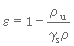(3. 5)
En utilisant la masse unitaire sèche maximale, on trouve la porosité minimale, et en utilisant la masse unitaire sèche minimale, on trouve la porosité maximale.
On peut mesurer la porosité dans un cylindre de verre ou de plastique, de diamètre intérieur D, dans lequel on verse une hauteur h de milieu filtrant. On obtient la valeur de la porosité de la façon décrite ci-dessous.
On sait que
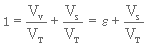(3. 6)
et que
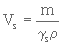(3. 7)
où
- m = masse de matériau sec dans la colonne (kg)
- ρ = masse volumique de l'eau (kg/m3)
Or
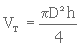(3. 8)
Par conséquent, en remplaçant, dans l'équation 3. 6, vs et vT (équat. 3. 7 et 3. 8) par leurs valeurs, on obtient
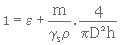(3. 9)
soit
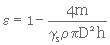(3. 10)
