3.3.2.1. Ιquation de Carman-Kozeny
En supposant que le processus de filtration est semblable à l'écoulement d'un fluide à travers d'innombrables petits tubes verticaux, on peut calculer la perte de charge due au frottement à l'aide de l'équation de Darcy-Weisbach
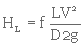 (3. 11)
(3. 11)
où
- HL = perte de charge à travers un tube de longueur L
- V = vitesse moyenne d'écoulement du liquide dans le tube
- D = diamètre du tube
- f = coefficient de friction
- g = accélération due à la pesanteur
Puisqu'il est impossible de déterminer le diamètre D, on le remplace par une expression dans laquelle il est fonction du rayon hydraulique. Par définition, le rayon hydraulique, Rh , est
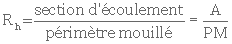
Or, pour un tube, 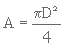 et PM = πD.
et PM = πD.
Donc 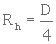 et D = 4.Rh
et D = 4.Rh
En remplaçant D par cette valeur dans l'équation 3. 11, on obtient
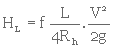 (3. 12)
(3. 12)
De plus, en multipliant Rh par 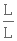 , on trouve que
, on trouve que
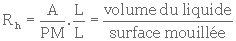 (3. 13)
(3. 13)
Or, puisque le volume du liquide est égal au volume des vides, on peut écrire
Volume du liquide = volume total. porosité
soit
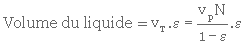 (3. 14)
(3. 14)
où
- vp = volume d'une particule
- N = nombre de particules
Par ailleurs, on sait que
Surface mouillée = As = Na (3. 15 )
Où
- a = surface d'une particule
- As = surface de l'ensemble des particules
En remplaçant, dans l'équation 3. 13, le volume du liquide (équat. 3. 14) et la surface mouillée (équat. 3.15) par leurs valeurs, on obtient
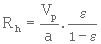 (3. 16)
(3. 16)
a) Lorsque le milieu filtrant est composé de particules sphériques de même diamètre d, on peut écrire
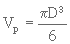 (3. 17)
(3. 17)
et
a = πD2 (3. 18)
d'où
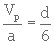 (3. 19)
(3. 19)
Par contre, lorsque le milieu filtrant est composé de particules non sphériques, il faut introduire un facteur de forme, Φ , sans dimension; on a alors
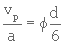 (3. 20)
(3. 20)
Il est par ailleurs facile de montrer que
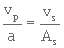 (3. 21)
(3. 21)
En remplaçant, dans l'équation 3. 16, 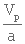 par cette valeur, on obtient
par cette valeur, on obtient
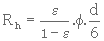 (3. 22)
(3. 22)
On calcule la charge superficielle, U, qui s'exerce sur un filtre à l'aide de l'équation de continuité
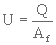 (3. 23)
(3. 23)
où Af est la surface totale du filtre et Q, le débit.
Lorsque le liquide pénètre dans le milieu filtrant, sa surface d'écoulement est réduite, à cause de la présence des particules. Il s'ensuit que la vitesse d'écoulement du liquide dans le filtre augmente; elle devient
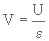 (3. 24)
(3. 24)
En remplaçant, dans l'équation 3. 12, Rh et V par leurs valeurs (équat. 3. 22 et 3. 24), on obtient l'équation de Carman-Kozeny
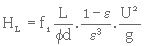 (3. 25)
(3. 25)
dans laquelle le facteur sans dimension, f1, est obtenu à l'aide de la formule empirique suivante :
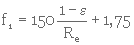 (3. 26)
(3. 26)
où
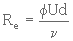 (3. 27)
(3. 27)
Re est appelé pseudo-nombre de Reynolds.
b) Lorsque le milieu filtrant est homogène et composé de particules de diamètres variés, on remplace, dans l'équation 3. 25, le diamètre des particules par 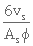 (équat. 3. 20). On obtient alors
(équat. 3. 20). On obtient alors
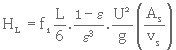 (3. 28)
(3. 28)
Le facteur de forme est éliminé, ce qui est logique, puisque le rapport 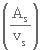 est valable pour n'importe quelle forme de particules. Cependant, A s représente ici la surface totale des particules contenues dans le milieu et v s , le volume de l'ensemble des particules. La valeur de A s étant difficile à mesurer, on évalue plutôt le rapport
est valable pour n'importe quelle forme de particules. Cependant, A s représente ici la surface totale des particules contenues dans le milieu et v s , le volume de l'ensemble des particules. La valeur de A s étant difficile à mesurer, on évalue plutôt le rapport 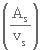 de la façon suivante :
de la façon suivante :
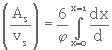 (3. 29)
(3. 29)
où dx est .la fraction des particules de diamètre d.
Puisqu'on connaît, par tamisage, les caractéristiques granulométriques du milieu filtrant, on peut écrire
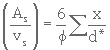 (3. 30)
(3. 30)
où
- x = fraction (en masse) des particules retenues entre deux tamis consécutifs
- d * = diamètre géométrique moyen des mailles de ces deux tamis
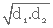
c) Après de nombreux lavages, le milieu filtrant peut être stratifié, les particules fines s'accumulant sur le dessus et les grosses particules se concentrant au fond du filtre (toutes les particules ont la même masse volumique).
En supposant que la porosité est constante dans le milieu et que le facteur de forme f est le même pour toutes les particules, on obtient, en dérivant l'équation 3. 25,
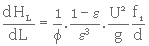 (3. 31)
(3. 31)
Seules les valeurs de f1 et de d sont variables f1 est fonction de Re , qui est fonction de d). L'équation suivante permet de calculer la perte de charge pour toute l'épaisseur du milieu :
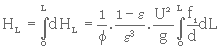 (3. 32)
(3. 32)
Or, dL = L.dx, dx étant la fraction des particules de diamètre d. L'équation 3. 32 devient donc
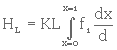 (3. 33)
(3. 33)
À partir des caractéristiques granulométriques du milieu, obtenues par tamisage, on peut écrire
 (3. 34)
(3. 34)
où
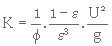 (3. 35)
(3. 35)
3.3.2.2. Ιquation de Rose
Cette équation, établie expérimentalement, fait intervenir le coefficient de traînée, CD , applicable aux particules sphériques.
Lorsque le milieu filtrant est composé de particules de même diamètre, on a
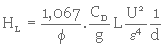 (3. 36)
(3. 36)
Pour un nombre de Reynolds (Re), compris entre 1 et 10 4 , le coefficient de traînée est 24 3
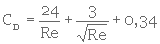 (3. 37)
(3. 37)
Lorsque Re ≤ 1, on peut estimer CD en ne recourant qu'au premier terme de l'équation 3. 37 ; ainsi
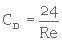 (3. 38)
(3. 38)
Rappelons qu'on calcule le nombre de Reynolds à l'aide de la formule suivante:
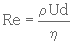 (3. 39)
(3. 39)
Lorsque le milieu filtrant est homogène et composé de particules de diamètres variés, on a
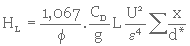 (3. 40)
(3. 40)
et, lorsque le milieu filtrant est stratifié,
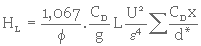 (3. 41)
(3. 41)
Le facteur de forme f est difficile à mesurer, étant donné qu'il varie d'une particule de sable à l'autre; il faut, par conséquent, utiliser une valeur qui soit représentative du milieu entier. On estime donc ce facteur f expérimentalement.
Toutefois, pour un même matériau filtrant, sa valeur peut être différente selon la formule employée !
Ainsi, Carman-Kozeny a trouvé pour :
Le charbon pulvérisé |
f = 0,73 |
Le sable Ottawa |
f= 0,95 |
Le sable Iowa (anguleux), |
f= 0,73 |
Rose, quant à lui, propose dans un de ses articles pour :
Le charbon pulvérisé |
f = 0,60 |
Le sable Ottawa |
f = 0,80 |
Le sable Iowa (anguleux), |
f = 0,70 |
Exemple 3. 2 :
Calculer la perte de charge par unité d'épaisseur à travers un milieu filtrant constitué d'un sable dont les caractéristiques granulométriques sont présentées au Tableau 3. 4.
La température de l'eau est de 4°C et sa viscosité cinématique, ν, est de 1,568.10-6 m²/s. Evaluer la perte de charge pour chacun des cas suivants ci-dessous.
- Sable homogène dont la porosité est de 0,394, le facteur de forme de 1 et la densité de 2,65. La charge superficielle est de 0,39 m/h (1,08.10-4 m/s).
- Mêmes conditions qu'en a), mais avec stratification.
- Mêmes conditions qu'en a), mais avec une charge superficielle de 5,83 m/h (1,62.10-3 m/s).
- Mêmes conditions qu'en c), mais avec stratification.
- Mêmes conditions qu'en d), mais avec une porosité de 0,414.
Tableau 3. 4 : Caractéristiques granulométriques d'un milieu filtrant (exp. 3. 2)
N° de Tamis (Tyler) |
Dimension des mailles de chaque tamis (mm) |
Pourcentage qui traverse chaque tamis |
14
20
28
32
35
42
48
60
65
100 |
1,168
0,833
0,589
0,495
0,417
0,347
0,295
0,246
0,208
0,147 |
100,0
99,1
94,3
79,7
61,8
44,3
24,5
9,1
2,0
0 |
Solution
| On trace, sur papier semi-logarithmique (Figure 3. 2), la variation du pourcentage des grains qui traversent chaque tamis en fonction du diamètre des mailles des tamis.
Sur cette courbe, on lit les valeurs du diamètre effectif (DE = 0,25 mm) et du coefficient d'uniformité (Cu = 1,6). |
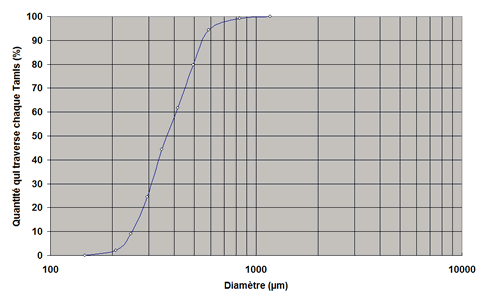
Figure 3. 2 : Courbes granulométriques d'un sable (exp. 3. 2)
|
Ce sable est plus fin que celui qu'on utilise en général dans les filtres rapides (DE = 0,4 à 0,55 mm). Par contre, pour les filtres lents, on recommande d'utiliser un sable dont les particules ont un diamètre effectif de 0,25 à 0,35 mm, avec un coefficient d'uniformité de 2 à 3. Le sable de cet exemple devrait donc être utilisé dans un filtre lent, même si son coefficient d'uniformité est plus faible que recommandé.
a) On doit calculer la perte de charge par unité d'épaisseur, HL/L, pour un milieu filtrant homogène composé de particules de diamètres variés. Avant de calculer la valeur de HL/L (équat. 3. 28), on doit procéder selon les étapes présentées ci-contre.
1- Calcul de As/vs
Les résultats obtenus sont présentés au Tableau 3. 5. On peut alors calculer la valeur de As/vs à l'aide de l'équation 3. 30 ; ainsi
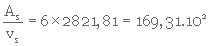
Tableau 3. 5 : Calcul de 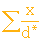 (exp. 3. 2)
(exp. 3. 2)
N° de Tamis (Tyler) |
Diamètre géométrique moyen (100d * , m) |
Pourcentage de l'échantillon retenu entre deux tamis consécutifs (100 x) |
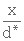 (m-1 ) (m-1 )
|
14 20
20 28
28 32
32 35
35 42
42 48
48 60
60 65
65 100 |
0,099
0,070
0,054
0,045
0,038
0,032
0,027
0,023
0,017 |
0,9
4,8
14,6
17,9
17,5
19,8
15,4
7,1
2,0
_________
100,00 |
9,09
68,57
270,37
397,78
460,53
618,75
570,37
308,70
117,65
___________
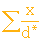 = 2821,81 = 2821,81
|
2- Calcul de Re (équat. 3. 27)
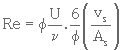
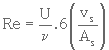
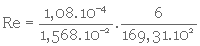
Re = 2,44.10-2
3- Calcul de f1, (équat. 3. 26)
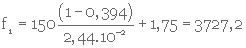
4- Calcul de la perte de charge par unité d'épaisseur (équat. 3. 28)
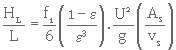
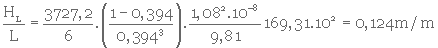
b) On peut calculer la perte de charge par unité d'épaisseur, pour un milieu filtrant stratifié, en utilisant les équations 3. 34 et 3. 35. On procède comme suit.
1- Calcul de 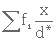
Les résultats des calculs suivants sont présentés au Tableau 3. 6.
Tableau 3. 6 : Calcul de 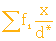 (exp. 3. 2b)
(exp. 3. 2b)
N° de Tamis (Tyler) |
Diamètre géométrique moyen (100d* , m) |
% retenu entre deux tamis consécutifs (100 x) |
Re |
f1 |
f1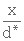 |
14 20
20 28
28 32
32 35
35 42
42 48
48 60
60 65
65 100 |
0,099
0,070
0,054
0,045
0,038
0,032
0,027
0,023
0,017 |
0,9
4,8
14,6
17,9
17,5
19,8
15,4
7,1
2,0 |
0,068
0,048
0,037
0,031
0,026
0,022
0,019
0,016
0,012 |
1338,52
1895,50
2458,51
2934,01
3497,90
4133,57
4785,96
5683,00
7576,75 |
12,17.10 3
129,98.10 3
664,71.10 3
1167,08.10 3
1610,88.10 3
2557,65.10 3
2729,77.10 3
1754,32.10 3
841,86.10 3 |
| |
|
_________
100,00 |
|
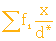 = 2821,81 = 2821,81 |
On sait que (équat. 3. 27)
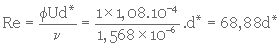
et que (équat. 3. 26)
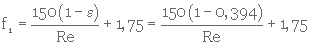
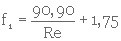
2- Calcul de K (équat. 3. 35)
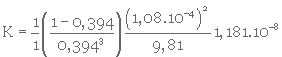
3- Calcul de HL/L (équat. 3. 34)
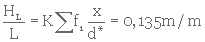
c) Pour calculer la perte de charge par unité d'épaisseur du milieu filtrant, on procède comme suit.
La valeur As/vs est la même que dans le cas a), soit 169,31.102
Calcul de Re
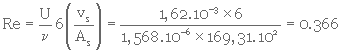
Calcul de f1
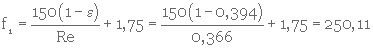
Calcul de la perte de charge unitaire, HL/L
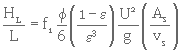
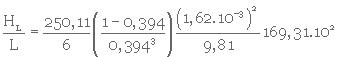
HL =1,871 m/m
d) On doit calculer la perte de charge par unité d'épaisseur lorsque le milieu est stratifié et que la charge superficielle est de 1,62.10 -3 m/s. On procède de la même manière que pour le cas b).
1- Calcul de 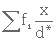
Les résultats des calculs sont présentés au Tableau 3. 7.
Tableau 3. 7 : Calcul de 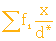 (exp. 3. 2d)
(exp. 3. 2d)
N° de Tamis (Tyler) |
Diamètre géométrique moyen (100d * , m) |
% retenu entre deux tamis consécutifs (100 x) |
Re |
f1 |
f1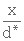 |
14 20
20 28
28 32
32 35
35 42
42 48
48 60
60 65
65 100 |
0,099
0,070
0,054
0,045
0,038
0,032
0,027
0,023
0,017 |
0,9
4,8
14,6
17,9
17,5
19,8
15,4
7,1
2,0 |
1,023
0,723
0,558
0,465
0,393
0,331
0,279
0,238
0,176 |
90,61
127,48
164,65
197,23
233,05
276,37
327,56
383,68
518,23 |
823,73
8741,49
44516,48
78455,25
107325,66
171003,94
186830,52
118440,35
60968,28 |
| |
|
_________
100,00 |
|
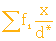 = 777105,70 = 777105,70 |
2- Calcul de la perte de charge
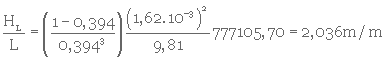
e) Les conditions de filtration sont les mêmes que pour le cas d), à l'exception de la porosité (0,414).
Les résultats des calculs sont présentés au Tableau 3. 8.
1- Calcul de 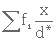
2- Calcul de HL/L
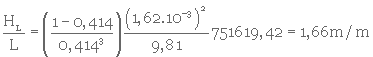
Tableau 3. 8 : Calcul de 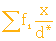 (exp. 3. 2e)
(exp. 3. 2e)
N° de Tamis (Tyler) |
Diamètre géométrique moyen (100d * , m) |
% retenu entre deux tamis consécutifs (100 x) |
Re |
f1 |
f1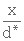 |
14 20
20 28
28 32
32 35
35 42
42 48
48 60
60 65
65 100 |
0,099
0,070
0,054
0,045
0,038
0,032
0,027
0,023
0,017 |
0,9
4,8
14,6
17,9
17,5
19,8
15,4
7,1
2,0 |
1,023
0,723
0,558
0,465
0,393
0,331
0,279
0,238
0,176 |
87,67
123,33
159,28
190,78
225,41
267,31
316,80
371,08
501,18 |
797,00
8456,91
43064,59
75888,94
103807,24
165398,06
180693,33
114550,78
58962,57 |
| |
|
_________
100,00 |
|
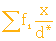 = 751619,42 = 751619,42 |
3.3.2.3. Ιcoulement vers le haut ΰ travers un milieu granuleux
Pour laver un filtre, on inverse le sens de l'écoulement. Lorsque la vitesse ascendante atteint une valeur critique, Vc , les particules sont soulevées; elles ne sont plus en contact les unes avec les autres et elles adoptent une position d'équilibre pour laquelle leur masse dans le liquide est égale à la force de traînée exercée par celui-ci. On dit que le milieu est fluidisé. L'écoulement devient en général turbulent (avec les matériaux granuleux usuels utilisés pour une filtration rapide), la position des particules n'est plus stable et une forte agitation entraîne les chocs des particules entre elles, ce qui favorise le détachement des saletés retenues sur les particules au cours de la filtration. À cette micro-agitation s'ajoute souvent une macro-turbulence qui provoque de forts mouvements de bascule dans le milieu. Ces mouvements ont probablement tendance à brasser le milieu, ce qui brise la stratification qu'on croit exister dans des milieux ainsi lavés. Toutefois, les critères théoriques qui définissent ces phénomènes ont été peu étudiés. Rappelons simplement que, bien qu'il soit logique de supposer qu'il y ait stratification d'un milieu après plusieurs lavages, ce n'est pas nécessairement le cas.
On peut calculer le degré d'expansion d'un milieu filtrant composé de particules de même diamètre. Pour cela, on considère un filtre dont le matériau filtrant a une épaisseur L et dont le fond est séparé de la crête des goulot tes par une hauteur h. La pression hydrostatique au fond du filtre est de ρLh. Lorsque l'écoulement a lieu vers le haut, avec une charge superficielle UL, le matériau filtrant prend de l'expansion et occupe une épaisseur Le. On a alors une suspension d'eau et de sable d'épaisseur Le surmontée d'une quantité d'eau d'épaisseur (h -Le). Le mélange eau-sable ayant une masse volumique supérieure à celle de l'eau, la pression hydrostatique au fond du lit est supérieure à ρLh. L'augmentation de pression est égale à hLρL, hL étant la perte de charge dans le filtre. On peut donc écrire
hL = (ρs-ρL)(1-εe)Le (3. 42)
où εe est la porosité du milieu en expansion.
On a donc
hL = (γs-1)(1-εe)Le (3. 43)
Puisque le volume des solides est conservé, on a
Le = (1-εe) = L(1-ε) (3. 44)
où ε est la porosité du milieu au repos.
On peut donc calculer hL à l'aide de l'équation suivante :
hL = (γs-1)(1-ε)L (3. 45)
On peut par ailleurs calculer l'épaisseur Le du milieu en expansion à l'aide de l'équation 3. 44 lorsqu'on connaît la porosité εe. Selon Fair et Geyer, le degré d'expansion d'un milieu filtrant est fonction de la charge superficielle (ou vitesse ascendante de l'eau), UL , et de la vitesse de chute des particules, Vp ; ils ont donc proposé la formule empirique suivante :
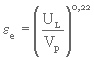 (3. 46)
(3. 46)
En combinant les équations 3. 44 et 3. 46, on obtient
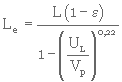 (3. 47)
(3. 47)
On peut en outre calculer le degré d'expansion d'un milieu filtrant stratifié en modifiant les équations ci-dessus.
Puisque, dans un milieu stratifié, l'expansion commence en haut, pour les particules les plus fines, et s'étend vers le bas au furet à mesure que le débit de l'eau de lavage augmente, le milieu est en expansion totale lorsque UL atteint une valeur suffisante (la charge superficielle critique, Uc ) pour fluidiser les plus grosses particules. On calcule la valeur de cette charge superficielle à l'aide de l'équation 3. 46; on obtient
Uc =Vp ε 4,5 (3. 48 )
Avec cette équation, puisqu'on utilise la porosité initiale du milieu filtrant, on calcule la charge superficielle, Uc , suffisante pour soulever les plus grosses particules. Cette charge est donc nécessairement suffisante pour soulever également les particules des strates supérieures. La porosité, εe est différente dans chacune des strates; elle dépend de la vitesse de chute des particules. On peut calculer l'épaisseur du milieu filtrant en expansion à l'aide de l'équation suivante :
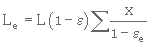 (3. 49)
(3. 49)
Exemple 3. 3 :
Calculer la perte de charge et la hauteur Le du milieu filtrant en expansion lorsque la vitesse des eaux de lavage, UL , est de 1,087 cm/s. Le milieu filtrant est constitué de billes de verre de densité relative 2,50; sa porosité est de 0,412 et son épaisseur de 61,6cm. La température de l'eau est de 20°C et sa viscosité cinématique de 1,003.10-2 cm2/s. Une analyse granulométrique de ce milieu filtrant a donné les résultats présentés au Tableau 3. 9.
Tableau 3. 9 : Résultats de l'analyse granulométrique d'un milieu filtrant (exp. 3. 3)
N° de Tamis (Tyler) |
Diamètre géométrique moyen (mm) |
Pourcentage de l'échantillon retenu entre deux tamis consécutifs (100 x) |
20 25
25 30
30 35
35 40 |
0,771
0,646
0,539
0,454 |
1,29
83,90
14,76
0,05
_________
100,00 |
Solution
1- Calcul de la vitesse de chute, Vp , des particules
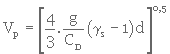
Lorsque le nombre de Reynolds est situé entre 1,9 et 500, on peut estimer CD à l'aide de l'expression suivante :
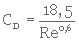 (3. 50 )
(3. 50 )
A partir des deux expressions ci-dessus, on trouve donc
Vp = 201d1,14 (cm/s) (3. 51 )
2- Calcul de la porosité du milieu en expansion (équat. 3. 46)
3- Calcul de 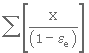
Les résultats des calculs précédents sont présentés au Tableau 3. 10.
Tableau 3. 10 : Calcul de 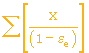
N° de Tamis (Tyler) |
Diamètre géométrique moyen (mm) |
% retenu entre deux tamis consécutifs (100 x) |
Vitesse de Chute Vp (cm/s) |
Porosité εe |
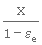
|
20 25
25 30
30 35
35 40 |
0,771
0,646
0,539
0,454 |
1,29
83,90
14,76
0,05
_________
100,00 |
10,83
8,85
7,20
5,92 |
060
0,63
0,66
0,69 |
0,032
2,268
0,434
0,002
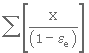 = 2,736 = 2,736
|
4- Vérification de l'expansion du milieu filtrant
Pour savoir si le milieu est en expansion, il faut étudier le comportement des plus grosses particules. On peut calculer la charge superficielle critique requise pour le soulèvement de ces particules à l'aide de l'équation 3. 48 (rappelons qu'il faut utiliser la porosité initiale du milieu, soit 0,412).
Uc = 10,83 x 0,4124,5 =0,200 cm/s
Or
UL >> Uc
puisque
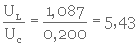
Les plus grosses particules seront donc fluidisées; par conséquent, le milieu entier le sera également.
5- Calcul de l'épaisseur du lit en expansion (équat. 3. 49)
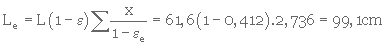
Le pourcentage d'expansion est donc
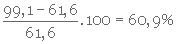
6- Calcul de la perte de charge (équat. 3. 45)
hL = (γs-1)(1-ε)L
hL = (2,5-1)(1-0,412)61,6
hL =54,33 cm
7- Vérification de la valeur du nombre de Reynolds (équat. 3. 39)
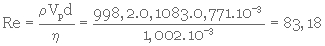
Les équations utilisées pour calculer la vitesse de chute des particules sont donc bien applicables à ce cas.

