L'équation de DARCY n'est pas directement applicable aux fluides compressibles puisque dans ce cas, le débit volumique est variable. Par contre, le produit :
Φ = um.p (ou encore Φ = q v.p)
reste constant à température constante.
La loi de DARCY devient alors :
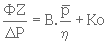
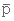est la moyenne des pressions d'entrée p1 et de sortie p2 du milieu poreux de perméabilité B.
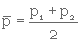
ΔP = p1 - p2
η est la viscosité du gaz
et Ko une constante permettant de tenir compte du fait que l'écoulement d'un gaz aux pressions ordinaires est un écoulement glissant et non visqueux. Ce qui signifie que la vitesse des molécules de gaz en contact avec les parois des pores n'est pas nulle comme c'est le cas pour les molécules de liquides.
Ko peut être calculée à partir de la relation proposée par CARMAN
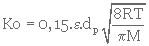
où R est la constante des gaz parfaits.
- R = 8,31 joule (K)-1 (mole)-1
- ε est la porosité du milieu poreux
- M la masse molaire
- T la température en KELVIN
