Soit un tube dont l'aire de la section est S rempli sur une longueur Z par un milieu poreux, par exemple du sable.
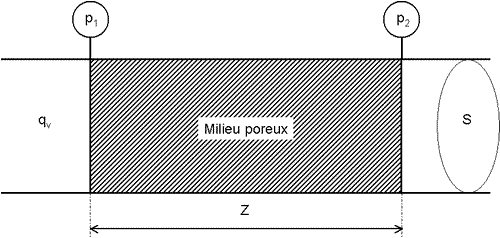
Ce milieu poreux est traversé en régime permanent par un débit volumique de liquide qV.
Deux manomètres placés respectivement à l'entrée et à la sortie du milieu poreux indiquent les pressions p
1 et p
2 . Nous appellerons
vitesse en fût vide.
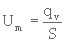
La vitesse en fût vide est la vitesse moyenne qu'aurait le liquide dans le tube en absence de milieu poreux. C'est aussi la vitesse moyenne d'approche du liquide.
Lorsque le régime d'écoulement est laminaire, la loi de DARCY s'écrit :
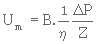
| η |
est la viscosité dynamique du liquide exprimée en Pl |
| ΔP = p1 - p2 |
est la chute de pression exprimée en Pascal |
| um |
la vitesse en fût vide est exprimée en m.s-1 |
| Z |
la longueur du milieu poreux s'exprime en m |
| B |
est la caractéristique du milieu poreux, c'est la perméabilité du milieu. |
La dimension de la perméabilité est :
[B] = L2
Les valeurs des perméabilités rencontrées en filtration varient autour de 1 à 10-2 micromètre carré (μm2). Le μm2 correspond à peu près à 1 Darcy, unité de perméabilité réalisée à partir d'un système non homogène.
1 Darcy = 0,986.10-12 m2

