Le critère de Reynolds est un nombre adimensionnel définit comme suit :

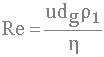(1.5)

• ρ_l est la masse volumique du fluide en kg.m^-3
• d_g est le diamètre de la particule sphèrique en m
• η est la viscosité du fluide en Pa.s
• u est la vitesse relative du fluide par rapport au grain exprimée en m.s^-1

On distingue, comme en mécanique des fluides, 3 régimes d'écoulement :

• Le régime laminaire ou régime de STOKES pour lequel Re_g<1
  
  

  Dans ce cas les lignes de courant suivent parfaitement le contour de l’obstacle sans en décoller. Les frottements sont alors uniquement dus à la viscosité du fluide.

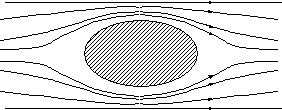
  Figure 1. 2 : cas du régime laminaire

  
  
  

   

   

   

  
  La traînée est donnée par la formule de STOKES

F_T = 3πηd_gu (1. 6)

• Le régime intermédiaire ou régime d'ALLEN pour lequel 1<Re_g<1000
  Dans ce cas et contrairement à ce qui se passe dans une canalisation, le régime intermédiaire
  
  

  couvre une gamme étendue de vitesse. On constate en régime intermédiaire qu'une microturbulence apparaît en aval de l'obstacle. Cette perturbation est d'autant plus importante que le critère de REYNOLDS tend vers sa limite supérieure (1000).

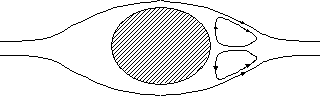
  Figure 1. 3 : cas du régime intermédiaire

  
  










La traînée est donnée par la formule :

F_T = 2,31 πη^0,6ρ_l^0,4d_g^1,4u^1,4 (1.7)

• Le régime turbulent ou régime de NEWTON pour lequel 1000<Re_g<4.10⁵.
  
  

  Dans ce cas, le sillage en aval de l'obstacle est entièrement turbulent.

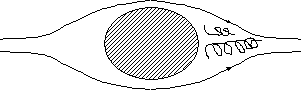
  Figure 1. 4 : cas du régime turbulent

  
  
  

  La traînée est donnée par l’équation de NEWTON :

  F_T = 0,055 πρ_ld_g²u² (1. 8)