Enoncé
1) Calculer pour des billes d'alumine de 3 mm, le volume, la surface et l'aire spécifique.
2) Calculer le nombre de billes d'alumine correspondant à 1 litre de matière ainsi que la surface totale correspondante.
3) Reprendre les mêmes questions pour des billes de polystyrènes de 150 μm de diamètre.
Correction
1) Une bille d'alumine a un diamètre (dg)1 = 0,3 cm
un volume 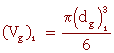
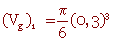
(Vg)1 = 0,014cm3
une surface (Ag)1 = π (dg)12
(Ag)1 = π x (0,3)2
(Ag)1 = 0,283 cm2
et une surface spécifique
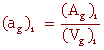
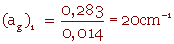
Remarque : En utilisant le diamètre d'une bille :
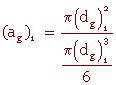
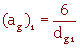
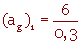
(ag)1 = 20cm-1
2) Le volume d'alumine solide est V = 103 cm3. Il correspond à N1 billes tel que :
V = N1.(Vg)1
ou 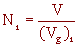
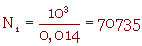
3) Les billes de polystyrène ont un diamètre :
(dg)2 = 1,5.10-2 cm
Un volume 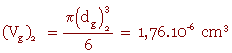
Une surface (Ag)21 = p (dg)22 = 7 069.10-4 cm2
Une surface spécifique 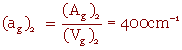
Remarque : La surface spécifique est 20 fois plus grande pour les billes de polystyrène que pour les billes d'alumine. Ce résultat peut être retrouvé avec la relation :
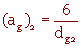
Pour le comprendre, calculons le nombre de billes de polystyrène contenues dans 1 litre :
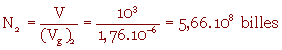
N2 est 8000 fois plus grand que N1.
En fait, 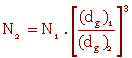
Alors que la surface d'une bille est 400 fois plus petite
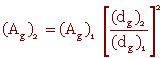
A volume de solide égale, la surface totale A 2 des billes de polystyrène est donc bien 20 fois plus grande que celle A 1 des billes d'alumine.
A2 = N2 (Ag)2
A1 = N1 (Ag)1
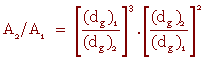
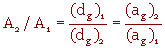
Conclusion : Plus la matière est divisée et plus elle offre de surface.

