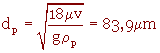Enoncé

Des particules de poussières ayant trois tailles différentes sédimentent dans l'air.
Déterminer la vitesse terminale de chute de chaque type de particules et déterminer quelle distance chacune de ces particules va parcourir après 30 secondes de chute.
Calculer le diamètre de la particule qui sédimentera à une vitesse de 0,422 m/s.
On suppose que les particules sont sphériques et on donne :

• Taille de particules : 0,4 – 40 et 400 µm
• Température de l'air : 100 °C
• Pression de l'air : 1atm
• Densité des poussières : 2,31

Correction

Soit le nombre adimensionnel k.

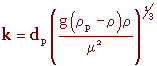
• d_p  : diamètre des particules
• g : accélération de la pesanteur
• ρ_p : masse volumique des particules
• ρ : masse volumique du gaz
• μ : viscosité du gaz

Si d_p est en m, g en m/s², ρ_p en kg/m³ et μ en kg/(m.s) on aura :

Pour le régime de Stokes :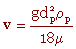

Pour le régime intermédiaire :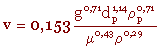

Et pour le régime de Newton :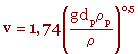

Pour les très fines particules, on introduit la correction de Cunningham pour l'estimation de la vitesse en régime de stokes : 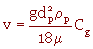, où C_g est le facteur de correction de Cunningham.

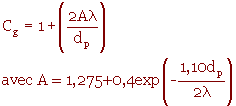
λ : libre parcours moyen pour les molécules de gaz ( λ = 6,5310 -6 cm pour l'air ambiant)

La correction de Cunningham est généralement appliquée pour les particules dont la taille est ≤1µm.

Dans notre cas

La masse volumique des particules est :
ρ_p = 2310 kg/m³

la densité de l'air est :
ρ = 0,911 kg/m³

la viscosité de l'air est :
μ = 0,021 cP=0,021.10 -3 Poiseuil (kg/(m.s))

On calcule k pour chaque type de particules sachant que (ρ_p - ρ_p ≈ ρ_p)

• Pour d_p = 0,4 µm : k=0,0144 régime de Stokes
• Pour d_p = 40 µm : k=1,44 régime de Stokes
• Pour d_p = 400 µm : k=14,4 rségime intermédiaire

Donc

• pour d_p = 0,4 µm : v=0,9610^-5 m/s (sans la correction de Cunningham)
• pour d_p = 40 µm : v=0,096 m/s
• pour d_p = 400 µm : v=2,71 m/s

Distance parcourue après 30 secondes

• pour d_p =40 µm : distance=2,88 m
• pour d_p =400 µm : distance=81,38 m
• pour d_p =0,4 µm, on doit tenir compte de la correction de Cunningham
  C_f =1,415 vitesse corrigée=1,36.10^-5 m/s distance parcourue=0,41.10^-3 m

Pour la détermination du diamètre de particule connaissant la vitesse terminale de chute on peut procéder de deux manières différentes :

1. essai erreur : on suppose qu'on est en régime de Stokes, connaissant v on détermine d_p on calcule ensuite k et on vérifie bien qu'on est en régime de Stokes
   
   
2. Larocca (Chem. Eng. N°2, Avril 87, pp 73) définit un nombre adimensionnel w qui permet de calculer le diamètre des particules connaissant la vitesse terminale de chute.
   w qui ne dépend pas de d_p est donné par : .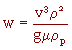
   w < 0,2222 : régime de Stokes
   0,2222 < w < 1514 : régime intermédiaire
   1514 <w : régime de Newton

Dans notre cas :

w=0,1312 < 0,2222, nous sommes donc en régime de Stokes